
【題目】某次數學知識比賽中共有6個不同的題目,每位同學從中隨機抽取3個題目進行作答,已知這6個題目中,甲只能正確作答其中的4個,而乙正確作答每個題目的概率均為![]() ,且甲、乙兩位同學對每個題目的作答都是相互獨立、互不影響的.
,且甲、乙兩位同學對每個題目的作答都是相互獨立、互不影響的.
(1)求乙同學答對2個題目的概率;
(2)若甲、乙兩位同學答對題目個數分別是m,n,分別求出甲、乙兩位同學答對題目個數m,n的概率分布和數學期望.
【答案】(1)![]() (2)詳見解析
(2)詳見解析
【解析】
(1)根據獨立重復事件的概率公式直接計算概率即可;
(2)由題可知,隨機變量m服從超幾何分布,所有可能取值為1,2,3;隨機變量n服從二項分布,所有可能取值為0,1,2,3;然后分別根據超幾何分布、二項分布求概率的方式逐一求出每個m、n的取值所對應的概率即可得分布列,進而求得數學期望.
(1)由題意知乙同學答對題目個數n~B(3,![]() ),
),
乙同學答對2個題目的概率為P![]() .
.
(2)甲同學答對題目個數m的所有可能取值1,2,3,
P(m=1)![]() ,P(m=2)
,P(m=2)![]() ,P(m=3)
,P(m=3)![]() .
.
∴m的分布列為

數學期望E(m)![]() .
.
乙同學答對題目個數n~B(3,![]() ),n的所有可能取值為0,1,2,3,
),n的所有可能取值為0,1,2,3,
P(n=0)![]() ,P(n=1)
,P(n=1)![]() ,
,
P(n=2)![]() ,P(n=3)
,P(n=3)![]() .
.
∴n的分布列為:

數學期望E(n)![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】在一個特定時段內,以點E為中心的7n mile以內海域被設為警戒水域.點E正北55n mile處有一個雷達觀測站A,某時刻測得一艘勻速直線行駛的船只位于點A北偏東45°且與點A相距40![]() n mile的位置B,經過40分鐘又測得該船已行駛到點A北偏東
n mile的位置B,經過40分鐘又測得該船已行駛到點A北偏東![]() (其中
(其中![]() ,
,![]() )且與點A相距10
)且與點A相距10![]() n mile的位置C.
n mile的位置C.
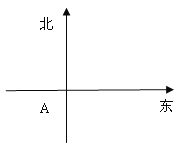
(I)求該船的行駛速度(單位:n mile /h);
(II)若該船不改變航行方向繼續行駛.判斷它是否會進入警戒水域,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確命題的個數是( )
(1)若函數![]() 的定義域
的定義域![]() 關于原點對稱,則
關于原點對稱,則![]() 為偶函數的充要條件為對任意的
為偶函數的充要條件為對任意的![]() ,
,![]() 都成立;
都成立;
(2)若函數![]() 的定義域
的定義域![]() 關于原點對稱,則“
關于原點對稱,則“![]() ”是“
”是“![]() 為奇函數”的必要條件;
為奇函數”的必要條件;
(3)函數![]() 對任意的實數
對任意的實數![]() 都有
都有![]() ,則
,則![]() 在實數集
在實數集![]() 上是增函數;
上是增函數;
(4)已知函數![]() 在其定義域內有兩個不同的極值點,則實數
在其定義域內有兩個不同的極值點,則實數![]() 的取值范圍是
的取值范圍是![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若α是第一象限角,則sinα+cosα的值與1的大小關系是( )
A. sinα+cosα>1B. sinα+cosα=1C. sinα+cosα<1D. 不能確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》(第三季)亮點頗多,在“人生自有詩意”的主題下,十場比賽每場都有一首特別設計的開場詩詞在聲光舞美的配合下,百人團齊聲朗誦,別有韻味.若《沁園春·長沙》、《蜀道難》、《敕勒歌》、《游子吟》、《關山月》、《清平樂·六盤山》排在后六場,且《蜀道難》排在《游子吟》的前面,《沁園春·長沙》與《清平樂·六盤山》不相鄰且均不排在最后,則后六場的排法有__________種.(用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2012年12月18日,作為全國首批開展空氣質量新標準監測的74個城市之一,鄭州市正式發布![]() 數據.資料表明,近幾年來,鄭州市霧霾治理取得了很大成效,空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數(
數據.資料表明,近幾年來,鄭州市霧霾治理取得了很大成效,空氣質量與前幾年相比得到了很大改善.鄭州市設有9個監測站點監測空氣質量指數(![]() ),其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點,以9個站點測得的
),其中在輕度污染區、中度污染區、重度污染區分別設有2,5,2個監測站點,以9個站點測得的![]() 的平均值為依據,播報我市的空氣質量.
的平均值為依據,播報我市的空氣質量.
(Ⅰ)若某日播報的![]() 為118,已知輕度污染區
為118,已知輕度污染區![]() 的平均值為74,中度污染區
的平均值為74,中度污染區![]() 的平均值為114,求重度污染區
的平均值為114,求重度污染區![]() 的平均值;
的平均值;
(Ⅱ)如圖是2018年11月的30天中![]() 的分布,11月份僅有一天
的分布,11月份僅有一天![]() 在
在![]() 內.
內.
組數 | 分組 | 天數 |
第一組 |
| 3 |
第二組 |
| 4 |
第三組 |
| 4 |
第四組 |
| 6 |
第五組 |
| 5 |
第六組 |
| 4 |
第七組 |
| 3 |
第八組 |
| 1 |
①鄭州市某中學利用每周日的時間進行社會實踐活動,以公布的![]() 為標準,如果
為標準,如果![]() 小于180,則去進行社會實踐活動.以統計數據中的頻率為概率,求該校周日進行社會實踐活動的概率;
小于180,則去進行社會實踐活動.以統計數據中的頻率為概率,求該校周日進行社會實踐活動的概率;
②在“創建文明城市”活動中,驗收小組把鄭州市的空氣質量作為一個評價指標,從當月的空氣質量監測數據中抽取3天的數據進行評價,設抽取到![]() 不小于180的天數為
不小于180的天數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() 是
是![]() 軸與圓
軸與圓![]() 的一個公共點(異于原點),拋物線
的一個公共點(異于原點),拋物線![]() 的準線為
的準線為![]() ,
,![]() 上橫坐標為
上橫坐標為![]() 的點
的點![]() 到
到![]() 的距離等于
的距離等于![]() .
.
(1)求![]() 的方程;
的方程;
(2)直線![]() 與圓
與圓![]() 相切且與
相切且與![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() 的面積為4,求
的面積為4,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com