
【題目】設函數![]() 是定義域R上的奇函數.
是定義域R上的奇函數.
(1)設![]() 是
是![]() 圖像上的兩點,求證:直線AB的斜率>0;
圖像上的兩點,求證:直線AB的斜率>0;
(2)求函數![]() 在區間
在區間![]() 上的最大值.
上的最大值.
【答案】(1)證明見解析;(2)當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
【解析】
(1)由函數是奇函數可利用![]() 進行
進行![]() 值求解;可利用增函數的定義求證函數
值求解;可利用增函數的定義求證函數![]() 是增函數,即直線AB的斜率>0
是增函數,即直線AB的斜率>0
(2)先利用(1)的結論,設![]() ,由
,由![]() 在
在![]() 遞增,可得
遞增,可得![]() ,
,![]() 可化簡為
可化簡為![]() ,設
,設![]() ,對稱軸
,對稱軸![]() ,討論對稱軸與定義域的關系可進一步求得
,討論對稱軸與定義域的關系可進一步求得![]() 最值
最值
(1)由![]() ,因為函數
,因為函數![]() 是定義域R上的奇函數,所以
是定義域R上的奇函數,所以![]() ,即
,即![]() ,原表達式為
,原表達式為![]()
設![]() 是
是![]() 圖像上的兩點,且
圖像上的兩點,且![]() ,
,
則![]() ,因為
,因為![]() 在
在![]() 上單調遞增,所以
上單調遞增,所以![]() ,又因為
,又因為![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上為增函數,即直線AB的斜率>0
上為增函數,即直線AB的斜率>0
(2)設![]() ,由
,由![]() ,可得
,可得![]() ,由
,由![]() 在
在![]() 遞增,可得
遞增,可得![]() ,由
,由![]() ,即有函數
,即有函數![]()
![]() ,對稱軸
,對稱軸![]()
當對稱軸![]() ,即
,即![]() 時,可得
時,可得![]() 時,即
時,即![]() ,最大值為2;
,最大值為2;
當對稱軸![]() ,即
,即![]() 時,可得
時,可得![]() 時,即
時,即![]() 時,取得最大值
時,取得最大值![]() ;
;
綜上所述,當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設橢圓![]() :
:![]() (
(![]() ),左、右焦點分別是
),左、右焦點分別是![]() 、
、![]() 且
且![]() ,以
,以![]() 為圓心,3為半徑的圓與以
為圓心,3為半徑的圓與以![]() 為圓心,1為半徑的圓相交于橢圓
為圓心,1為半徑的圓相交于橢圓![]() 上的點
上的點![]()
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓![]() :
:![]() ,
,![]() 為橢圓
為橢圓![]() 上任意一點,過點
上任意一點,過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,射線
兩點,射線![]() 交橢圓
交橢圓![]() 于點
于點![]()
①求![]() 的值;
的值;
②令![]() ,求
,求![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設n為正整數,集合A=![]() .對于集合A中的任意元素
.對于集合A中的任意元素![]() 和
和![]() ,記
,記
M(![]() )=
)=![]() .
.
(Ⅰ)當n=3時,若![]() ,
, ![]() ,求M(
,求M(![]() )和M(
)和M(![]() )的值;
)的值;
(Ⅱ)當n=4時,設B是A的子集,且滿足:對于B中的任意元素![]() ,當
,當![]() 相同時,M(
相同時,M(![]() )是奇數;當
)是奇數;當![]() 不同時,M(
不同時,M(![]() )是偶數.求集合B中元素個數的最大值;
)是偶數.求集合B中元素個數的最大值;
(Ⅲ)給定不小于2的n,設B是A的子集,且滿足:對于B中的任意兩個不同的元素![]() ,
,
M(![]() )=0.寫出一個集合B,使其元素個數最多,并說明理由.
)=0.寫出一個集合B,使其元素個數最多,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A是同時符合以下性質的函數f(x)組成的集合:
①x∈[0,+∞),都有f(x)∈(1,4];②f(x)在[0,+∞)上是減函數.
(1)判斷函數f1(x)=2-![]() 和f2(x)=1+3·
和f2(x)=1+3·![]() (x≥0)是否屬于集合A,并簡要說明理由;
(x≥0)是否屬于集合A,并簡要說明理由;
(2)把(1)中你認為是集合A中的一個函數記為g(x),若不等式g(x)+g(x+2)≤k對任意的x≥0總成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的上下兩個焦點分別為
的上下兩個焦點分別為![]() ,過點
,過點![]() 與
與![]() 軸垂直的直線交橢圓
軸垂直的直線交橢圓![]() 于
于![]() 兩點,
兩點, ![]() 的面積為
的面積為![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知![]() 為坐標原點,直線
為坐標原點,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() 兩個不同的點,若
兩個不同的點,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中:
①若![]() ,滿足
,滿足![]() ,則
,則![]() 的最大值為
的最大值為![]() ;
;
②若![]() ,則函數
,則函數![]() 的最小值為
的最小值為![]()
③若![]() ,滿足
,滿足![]() ,則
,則![]() 的最小值為
的最小值為![]()
④函數![]() 的最小值為
的最小值為![]()
正確的有__________.(把你認為正確的序號全部寫上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知M為圓C:x2+y2-4x-14y+45=0上任意一點,且點Q(-2,3).
(1)求|MQ|的最大值和最小值;
(2)若M(m,n),求![]() 的最大值和最小值
的最大值和最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國海軍,正在以不可阻擋的氣魄向深藍進軍。在中國海軍加快建設的大背景下,國產水面艦艇噸位不斷增大、技術日益現代化,特別是國產航空母艦下水,航母需要大量高素質航母艦載機飛行員。為此中國海軍在全國9省9所優質普通高中進行海航班建設試點培育航母艦載機飛行員。2017年4月我省首屆海軍航空實驗班開始面向全省遴選學員,有10000名初中畢業生踴躍報名投身國防,經過文化考試、體格測試、政治考核、心理選拔等過程篩選,最終招收50名學員。培養學校在關注學員的文化素養同時注重學員的身體素質,要求每月至少參加一次野營拉練活動(下面簡稱“活動”)并記錄成績.10月某次活動中海航班學員成績統計如圖所示:
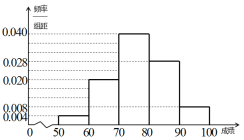
(Ⅰ)根據圖表,試估算學員在活動中取得成績的中位數(精確到![]() );
);
(Ⅱ)根據成績從![]() 、
、![]() 兩組學員中任意選出兩人為一組,若選出成績分差大于
兩組學員中任意選出兩人為一組,若選出成績分差大于![]() ,則稱該組為“幫扶組”,試求選出兩人為“幫扶組”的概率.
,則稱該組為“幫扶組”,試求選出兩人為“幫扶組”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com