
【題目】已知圓C:x2+y2+10x+10y+34=0.
(Ⅰ)試寫出圓C的圓心坐標和半徑;
(Ⅱ)圓D的圓心在直線x=-5上,且與圓C相外切,被x軸截得的弦長為10,求圓D的方程;
(Ⅲ)過點P(0,2)的直線交(Ⅱ)中圓D于E,F兩點,求弦EF的中點M的軌跡方程.
【答案】(Ⅰ)圓心坐標為(-5,-5),半徑為4;(Ⅱ)(x+5)2+(y-12)2=169;(Ⅲ)x2+y2+5x-14y+24=0.
【解析】試題分析:(Ⅰ)將圓的方程化為標準方程,即可得到圓心坐標和半徑;(Ⅱ)設圓![]() 的半徑為
的半徑為![]() ,圓心縱坐標為
,圓心縱坐標為![]() ,由已知條件列出方程,求出
,由已知條件列出方程,求出![]() 與
與![]() ,由此能求出圓
,由此能求出圓![]() 的方程;(Ⅲ)設
的方程;(Ⅲ)設![]() ,根據
,根據![]() 列出
列出![]() 且
且![]() ,化簡可得到
,化簡可得到![]() 的軌跡方程.
的軌跡方程.
試題解析:(Ⅰ)將圓的方程改寫為(x+5)2+(y+5)2=16,故圓心坐標為(-5,-5),半徑為4.
(Ⅱ)設圓D的半徑為r,圓心縱坐標為b,由條件可得r2=(r-1)2+52,解得r=13.
此時圓心縱坐標b=r-1=12.
所以圓D的方程為(x+5)2+(y-12)2=169.
(Ⅲ)設M(x,y),依題意有DM⊥PM.
即![]() (x≠0且x≠-5),
(x≠0且x≠-5),
整理得x2+y2+5x-14y+24=0(x≠0且x≠-5).
當x=0時,y=12,符合題意,當x=-5時,y=2,符合題意.
故所求點M的軌跡方程為x2+y2+5x-14y+24=0.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數f (x)的定義域是![]() ,對任意
,對任意![]()
當![]() 時,
時,![]() .關于函數
.關于函數![]() 給出下列四個命題:
給出下列四個命題:
①函數![]() 是奇函數;
是奇函數;
②函數![]() 是周期函數;
是周期函數;
③函數![]() 的全部零點為
的全部零點為![]() ;
;
④當![]() 時,函數
時,函數![]() 的圖象與函數
的圖象與函數![]() 的圖象有且只有三個公共點.
的圖象有且只有三個公共點.
其中真命題的個數為 .
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代秦九韶算法可計算多項式anxn+an﹣1xn﹣1+…+a1x+a0的值,它所反映的程序框圖如圖所示,當x=1時,當多項式為x4+4x3+6x2+4x+1的值為( ) 
A.5
B.16
C.15
D.11
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐S﹣ABCD中,底面ABCD為平行四邊形,側面SBC⊥面ABCD,已知∠ABC=45°,AB=2,BC=2 ![]() ,SB=SC=
,SB=SC= ![]() .
. 
(1)設平面SCD與平面SAB的交線為l,求證:l∥AB;
(2)求證:SA⊥BC;
(3)求直線SD與面SAB所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx。
(1)求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)求證:當x>0時,f(x)≥l-![]() ;
;
(3)若x-1>alnx對任意x>1恒成立,求實數a的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)判斷并證明函數![]() 的奇偶性;
的奇偶性;
(2)判斷當![]() 時函數
時函數![]() 的單調性,并用定義證明;
的單調性,并用定義證明;
(3)若![]() 定義域為
定義域為![]() ,解不等式
,解不等式![]() .
.
【答案】(1)奇函數(2)增函數(3)![]()
【解析】試題分析:(1)判斷與證明函數的奇偶性,首先要確定函數的定義域是否關于原點對稱,再判斷f(-x)與f(x)的關系,如果對定義域上的任意x,都滿足f(-x)=f(x)就是偶函數,如果f(-x)=-f(x)就是奇函數,否則是非奇非偶函數。(2)利函數單調性定義證明單調性,按假設,作差,化簡,判斷,下結論五個步驟。(3)由(1)(2)奇函數![]() 在(-1,1)為單調函數,
在(-1,1)為單調函數,
原不等式變形為f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函數的單調性及定義(-1,1)求解得x范圍。
試題解析:(1)函數![]() 為奇函數.證明如下:
為奇函數.證明如下:
![]() 定義域為
定義域為![]()
又![]()
![]() 為奇函數
為奇函數
(2)函數![]() 在(-1,1)為單調函數.證明如下:
在(-1,1)為單調函數.證明如下:
任取![]() ,則
,則


![]()
![]() ,
, ![]()

即![]()
故![]() 在(-1,1)上為增函數
在(-1,1)上為增函數
(3)由(1)、(2)可得
![]() 則
則
 解得:
解得: ![]()
所以,原不等式的解集為![]()
【點睛】
(1)奇偶性:判斷與證明函數的奇偶性,首先要確定函數的定義域是否關于原點對稱,再判斷f(-x)與f(x)的關系,如果對定義域上的任意x,都滿足f(-x)=f(x)就是偶函數,如果f(-x)=-f(x)就是奇函數,否則是非奇非偶函數。
(2)單調性:利函數單調性定義證明單調性,按假設,作差,化簡,定號,下結論五個步驟。
【題型】解答題
【結束】
22
【題目】已知函數![]() .
.
(1)若![]() 的定義域和值域均是
的定義域和值域均是![]() ,求實數
,求實數![]() 的值;
的值;
(2)若![]() 在區間
在區間![]() 上是減函數,且對任意的
上是減函數,且對任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() ,且對任意的
,且對任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右焦點分別是
的左、右焦點分別是![]() ,且點
,且點![]() 在
在![]() 上,拋物線
上,拋物線![]() 與橢圓
與橢圓![]() 交于四點
交于四點![]()
(I)求![]() 的方程;
的方程;
(Ⅱ)試探究坐標平面上是否存在定點![]() ,滿足
,滿足![]() ?(若存在,求出
?(若存在,求出![]() 的坐標;若不存在,需說明理由.)
的坐標;若不存在,需說明理由.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,正方形![]() 所在的平面與正三角形ABC所在的平面互相垂直,
所在的平面與正三角形ABC所在的平面互相垂直, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中點.
的中點.
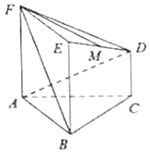
(1)求證: ![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com