
【題目】設橢圓C: ![]() ,定義橢圓C的“相關圓”方程為
,定義橢圓C的“相關圓”方程為![]() ,若拋物線
,若拋物線![]() 的焦點與橢圓C的一個焦點重合,且橢圓C短軸的一個端點和其兩個焦點構成直角三角形。
的焦點與橢圓C的一個焦點重合,且橢圓C短軸的一個端點和其兩個焦點構成直角三角形。
(I)求橢圓C的方程和“相關圓”E的方程;
(II)過“相關圓”E上任意一點P作“相關圓”E的切線l與橢圓C交于A,B兩點,O為坐標原點。
(i)證明∠AOB為定值;
(ii)連接PO并延長交“相關圓”E于點Q,求△ABQ面積的取值范圍。
【答案】(1) ![]() (2) (i)見解析(ii)
(2) (i)見解析(ii)![]()
【解析】試題分析:(Ⅰ)由拋物線![]() 的焦點與橢圓
的焦點與橢圓![]() 的一個焦點重合,且橢圓C短軸的一個端點和兩個焦點構成直角三角形,得到
的一個焦點重合,且橢圓C短軸的一個端點和兩個焦點構成直角三角形,得到![]() 由此能求出橢圓
由此能求出橢圓![]() 的方程.
的方程.
進而求出“相關圓”![]() 的方程.
的方程.
(Ⅱ)當直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 方程為
方程為![]() ;當直線
;當直線![]() 的斜率存在時,設其方程為
的斜率存在時,設其方程為![]() ,代入橢圓方程,得
,代入橢圓方程,得![]() 由此利用根的判別式、韋達定理、直線與圓相切,結合已知條件推導出
由此利用根的判別式、韋達定理、直線與圓相切,結合已知條件推導出![]() 為定值.
為定值.
(ii)要求![]() 的面積的取值范圍,只需求弦長
的面積的取值范圍,只需求弦長![]() 的范圍,由此利用橢圓弦長公式能求出
的范圍,由此利用橢圓弦長公式能求出![]() 面積的取值范圍.
面積的取值范圍.
試題解析:(Ⅰ)因為若拋物線![]() 的焦點為
的焦點為![]() 與橢圓
與橢圓![]() 的一個焦點重合,所以
的一個焦點重合,所以![]()
又因為橢圓![]() 短軸的一個端點和其兩個焦點構成直角三角形,所以
短軸的一個端點和其兩個焦點構成直角三角形,所以![]()
故橢圓![]() 的方程為
的方程為![]() ,
,
“相關圓”![]() 的方程為
的方程為![]()
(Ⅱ)(i)當直線![]() 的斜率不存在時,不妨設直線AB方程為
的斜率不存在時,不妨設直線AB方程為![]() ,
,
則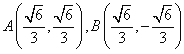 所以
所以![]()
當直線![]() 的斜率存在時,設其方程設為
的斜率存在時,設其方程設為![]() ,設
,設![]()
聯立方程組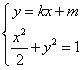 得
得![]() ,即
,即![]() ,
,
△=![]() ,即
,即![]()
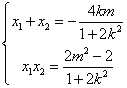
因為直線與相關圓相切,所以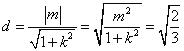
![]()
![]()
![]()
![]()
![]() 為定值
為定值
(ii)由于![]() 是“相關圓”的直徑,所以
是“相關圓”的直徑,所以![]() ,所以要求
,所以要求![]() 面積的取值范圍,只需求弦長
面積的取值范圍,只需求弦長![]() 的取值范圍
的取值范圍
當直線AB的斜率不存在時,由(i)知![]()
因為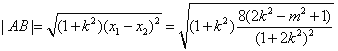
![]() ,
,
![]() 時
時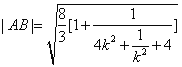 為
為![]() 所以
所以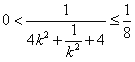 ,
,
所以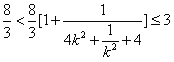 ,所以
,所以![]()
當且僅當![]() 時取”=”
時取”=”
②當![]() 時,
時,![]() .|AB |的取值范圍為
.|AB |的取值范圍為![]()
![]() 面積的取值范圍是
面積的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】已知命題p:k2﹣8k﹣20≤0,命題q:方程![]() 1表示焦點在x軸上的雙曲線.
1表示焦點在x軸上的雙曲線.
(1)命題q為真命題,求實數k的取值范圍;
(2)若命題“p∨q”為真,命題“p∧q”為假,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)一個盒子里裝有三張卡片,分別標記有數字![]() ,
,![]() ,
,![]() ,這三張卡片除標記的數字外完全相同。隨機有放回地抽取
,這三張卡片除標記的數字外完全相同。隨機有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 張,將抽取的卡片上的數字依次記為
張,將抽取的卡片上的數字依次記為![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的數字滿足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的數字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學舉行了一次“環保知識競賽”活動. 為了了解本次競賽學生成績情況,從中抽取了部分學生的分數(得分取正整數,滿分為100分)作為樣本(樣本容量為![]() )進行統計. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出了得分在[50,60),[90,100]的數據).
)進行統計. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(圖中僅列出了得分在[50,60),[90,100]的數據).
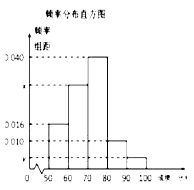

(1)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() ,
,![]() 的值;
的值;
(2)在選取的樣本中,從競賽成績是80分以上(含80分)的同學中隨機抽取3名同學到市政廣場參加環保知識宣傳的志愿者活動,設![]() 表示所抽取的3名同學中得分在[80,90)的學生人數,求
表示所抽取的3名同學中得分在[80,90)的學生人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 經過拋物線
經過拋物線![]() 與坐標軸的三個交點.
與坐標軸的三個交點.
(1)求圓![]() 的方程;
的方程;
(2)經過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交于
相交于![]() ,
,![]() 兩點,若圓
兩點,若圓![]() 在
在![]() ,
,![]() 兩點處的切線互相垂直,求直線
兩點處的切線互相垂直,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com