
已知函數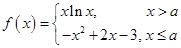 ,其中
,其中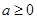 .
.
(1)當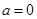 時,求函數
時,求函數 的圖象在點
的圖象在點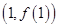 處的切線方程;
處的切線方程;
(2)如果對于任意 、
、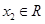 ,且
,且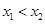 ,都有
,都有 ,求
,求 的取值范圍.
的取值范圍.
(1)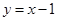 ;(2)
;(2)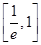 .
.
解析試題分析:(1)將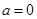 代入函數
代入函數 的解析式,求出切點坐標與
的解析式,求出切點坐標與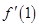 ,再利用點斜式寫出相應的切線方程;(2)將問題等價于
,再利用點斜式寫出相應的切線方程;(2)將問題等價于 在
在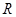 上單調遞增來處理,然后分別考慮函數
上單調遞增來處理,然后分別考慮函數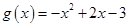 和
和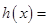
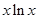 的單調性與極值,利用兩個函數的圖象確定直線
的單調性與極值,利用兩個函數的圖象確定直線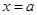 的位置,利用
的位置,利用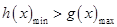 來進行限制,從而求解出實數
來進行限制,從而求解出實數 的取值范圍.
的取值范圍.
試題解析:(1)由題意,得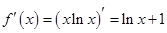 ,其中
,其中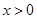 ,
,
所以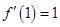 ,
,
又因為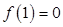 ,
,
所以函數 的圖象在點
的圖象在點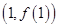 處的切線方程為
處的切線方程為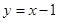 ;
;
(2)先考察函數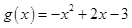 ,
,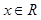 的圖象,
的圖象,
配方得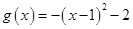 ,
,
所以函數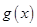 在
在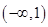 上單調遞增,在
上單調遞增,在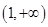 單調遞減,且
單調遞減,且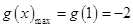 .
.
因為對于任意 、
、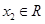 ,且
,且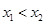 ,都有
,都有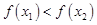 成立,
成立,
所以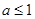 .
.
以下考察函數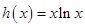 ,
,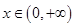 的圖象,
的圖象,
則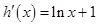 ,
,
令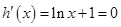 ,解得
,解得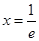 .
.
隨著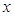 變化時,
變化時,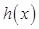 和
和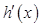 的變化情況如下:
的變化情況如下: