
【題目】已知函數![]() .
.
(1)當![]() 時,討論
時,討論![]() 的單調性;
的單調性;
(2)當![]() 時,若
時,若![]() ,證明:當
,證明:當![]() 時,
時, ![]() 的圖象恒在
的圖象恒在![]() 的圖象上方;
的圖象上方;
(3)證明: ![]() .
.
 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案科目:高中數學 來源: 題型:
【題目】已知: ![]() =(2sinx,2cosx),
=(2sinx,2cosx), ![]() =(cosx,﹣cosx),f(x)=
=(cosx,﹣cosx),f(x)= ![]() .
.
(1)若 ![]() 與
與 ![]() 共線,且x∈(
共線,且x∈( ![]() ,π),求x的值;
,π),求x的值;
(2)求函數f(x)的周期;
(3)若對任意x∈[0, ![]() ]不等式m﹣2≤f(x)≤m+
]不等式m﹣2≤f(x)≤m+ ![]() 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() sin ωxcos ωx-sin2ωx+1(ω>0)圖象的相鄰兩條對稱軸之間的距離為
sin ωxcos ωx-sin2ωx+1(ω>0)圖象的相鄰兩條對稱軸之間的距離為![]() .
.
(Ⅰ)求ω的值及函數f(x)的單調遞減區間;
(Ⅱ)如圖,在銳角三角形ABC中有f(B)=1,若在線段BC上存在一點D使得AD=2,且AC=![]() ,CD=
,CD=![]() -1,求三角形ABC的面積.
-1,求三角形ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線 ![]() (t為參數),
(t為參數), ![]() (
( ![]() 為參數).
為參數).
(1)化 ![]() ,
, ![]() 的方程為普通方程,并說明它們分別表示什么曲線;
的方程為普通方程,并說明它們分別表示什么曲線;
(2)過曲線 ![]() 的左頂點且傾斜角為
的左頂點且傾斜角為 ![]() 的直線
的直線 ![]() 交曲線
交曲線 ![]() 于
于 ![]() 兩點,求
兩點,求 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓錐曲線 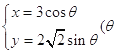 為參數)和定點
為參數)和定點 ![]() F1 , F2是圓錐曲線的左右焦點。
F1 , F2是圓錐曲線的左右焦點。
(1)求經過點F2且垂直于直線AF1的直線l的參數方程;
(2)以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,求直線AF2的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線 ![]() :
: 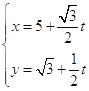 (t為參數).以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的坐標方程為
(t為參數).以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的坐標方程為 ![]() .
.
(1)將曲線C的極坐標方程化為直坐標方程;
(2)設點M的直角坐標為 ![]() ,直線l與曲線C的交點為A,B,求|MA||MB|的值.
,直線l與曲線C的交點為A,B,求|MA||MB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答
(1)設全集為R,A={x|3<x<7},B={x|4<x<10},求R(A∪B)及(RA)∩B.
(2)C={x|a﹣4≤x≤a+4},且A∩C=A,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,且離心率為
,且離心率為![]() ,點
,點![]() 為橢圓上一動點,
為橢圓上一動點, ![]() 內切圓面積的最大值為
內切圓面積的最大值為![]() .
.
(1)求橢圓的方程;
(2)設橢圓的左頂點為![]() ,過右焦點
,過右焦點![]() 的直線
的直線![]() 與橢圓相交于
與橢圓相交于![]() 兩點,連接
兩點,連接![]() 并延長分別交直線
并延長分別交直線![]() 于
于![]() 兩點,以
兩點,以![]() 為直徑的圓是否恒過定點?若是,請求出定點坐標;若不是,請說明理由.
為直徑的圓是否恒過定點?若是,請求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據氣象中心觀察和預測:發生于M地的沙塵暴一直向正南方向移動,其移動速度v(km/h)與時間t(h)的函數圖象如圖所示,過線段OC上一點T(t,0)作橫軸的垂線l,梯形OABC在直線l左側部分的面積即為t(h)內沙塵暴所經過的路程s(km). 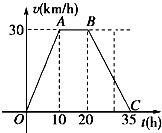
(1)當t=4時,求s的值;
(2)將s隨t變化的規律用數學關系式表示出來.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com