
���}Ŀ����֪�c(di��n)P(1,3)��Q(1,2).�O(sh��)�^�c(di��n)P�Ą�(d��ng)ֱ���c���タy=x2����A��B���c(di��n)��ֱ��AQ��BQ�cԓ���タ����һ���c(di��n)�քe��C��D.ӛֱ��AB��CD��б�ʷքe��k1��k2.
��1����(d��ng)![]() �r(sh��)������AB���L(zh��ng)��
�r(sh��)������AB���L(zh��ng)��
��2����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() �Ƿ�鶨ֵ�����ǣ����ԓ��ֵ.
�Ƿ�鶨ֵ�����ǣ����ԓ��ֵ.
���𰸡���1��![]() ����2���ǣ�
����2���ǣ�![]() .
.
��������
��1����(d��ng)![]() �r(sh��)������֪�c(di��n)
�r(sh��)������֪�c(di��n)![]() ������(bi��o)���Ƀ��c(di��n)֮�g�ľ��x��ʽ���ɵ����L(zh��ng)
������(bi��o)���Ƀ��c(di��n)֮�g�ľ��x��ʽ���ɵ����L(zh��ng)![]() ��
��
��2���O(sh��)��ֱ��![]() �ķ��̣�����(j��)�f�_(d��)���������
�ķ��̣�����(j��)�f�_(d��)���������![]() ����(bi��o)�cб��
����(bi��o)�cб��![]() ֮�g���P(gu��n)ϵ���O(sh��)��
֮�g���P(gu��n)ϵ���O(sh��)��![]() ������(bi��o)������(j��)
������(bi��o)������(j��)![]() ���c(di��n)�������ҵ�
���c(di��n)�������ҵ�![]() ����(bi��o)֮�g���P(gu��n)ϵ����Ƶصõ�
����(bi��o)֮�g���P(gu��n)ϵ����Ƶصõ�![]() ����(bi��o)֮�g���P(gu��n)ϵ�����ɱ�ʾ��
����(bi��o)֮�g���P(gu��n)ϵ�����ɱ�ʾ��![]() ���ٴ�ֵ�������C.
���ٴ�ֵ�������C.
��1����(d��ng)![]() �r(sh��)��ֱ��
�r(sh��)��ֱ��![]() �c���タ�Ľ��c(di��n)����(bi��o)��
�c���タ�Ľ��c(di��n)����(bi��o)��![]() �c
�c![]()
����![]() ���L(zh��ng)��
���L(zh��ng)��![]() ��
��
��2�����}�O(sh��)��ֱ��![]() ��
��![]()
(li��n)�����̽M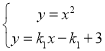 ����ȥ
����ȥ![]() ��
��![]()
����![]() ��
��![]()
���O(sh��)![]() ��
��
�t![]()
��![]() ���c(di��n)������
���c(di��n)������![]()
��![]() ��
��
ͬ��![]()
���ԣ���(d��ng)![]() �r(sh��)��
�r(sh��)��
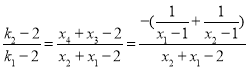
![]()
![]()
�ʮ�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() �鶨ֵ
�鶨ֵ![]()



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ij�H���Α�Y(ji��)���r(sh��)��һ�(xi��ng)�骄(ji��ng)���(d��ng)���骄(ji��ng)Ҏ(gu��)�t�ǣ��������湲��4��(g��)С��С���Ϸքe����0��1��2��3�Ĕ�(sh��)�֣�С�����(sh��)����������ȫ��ͬ��ÿ��(du��)�H���У����L(zh��ng)�ȏĺ�����ȡ��һ��(g��)С��ӛ��(sh��)�ֺ�С��Żأ�������?g��u)ĺ�����ȡ��һ��(g��)С��ӛ��С���ϔ�(sh��)��С��Żأ��骄(ji��ng)���(d��ng)�Ī�(ji��ng)��(l��)Ҏ(gu��)�t�ǣ�����ȡ���ăɂ�(g��)С���ϔ�(sh��)��֮�e����4���t��(ji��ng)��(l��)�w�C(j��)���һ��(g��)������ȡ���ăɂ�(g��)С���ϔ�(sh��)��֮�e�څ^(q��)�g��![]() ���t��(ji��ng)��(l��)��܇���һ��(g��)������ȡ���ăɂ�(g��)С���ϔ�(sh��)��֮�eС��1���t��(ji��ng)��(l��)���һƿ��
���t��(ji��ng)��(l��)��܇���һ��(g��)������ȡ���ăɂ�(g��)С���ϔ�(sh��)��֮�eС��1���t��(ji��ng)��(l��)���һƿ��
��1����ÿ��(du��)�H�ӫ@���w�C(j��)��ߵĸ��ʣ�
��2��ԇ���^ÿ��(du��)�H�ӫ@����܇����c�@����ϵĸ��ʣ��Ă�(g��)����Ո(q��ng)�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������FP��ABC�У�AB��1��BC��2��AC![]() ��PC
��PC![]() ��PA
��PA![]() ��PB
��PB![]() ��E�Ǿ���BC�����c(di��n)��
��E�Ǿ���BC�����c(di��n)��
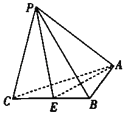
��1�����c(di��n)C��ƽ��APE�ľ��xd��
��2��������P��EA��B������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)�E�A![]() ������c(di��n)��
������c(di��n)��![]() ������c(di��n)��
������c(di��n)��![]() ����֪�E�A���x���ʞ�
����֪�E�A���x���ʞ�![]() �����Ծ���
�����Ծ���![]() ��ֱ���ĈA��ֱ��
��ֱ���ĈA��ֱ��![]() ���صõ����L(zh��ng)��
���صõ����L(zh��ng)��![]() ��
��
������E�A�Ę�(bi��o)��(zh��n)���̣�
�����O(sh��)�^�c(di��n)![]() ��ֱ��
��ֱ��![]() �c�E�A�����c(di��n)
�c�E�A�����c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �ڵ�һ���ޣ��c(di��n)
�ڵ�һ���ޣ��c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q�c(di��n)���c(di��n)
�S��(du��)�Q�c(di��n)���c(di��n)![]() ��ֱ��
��ֱ��![]() �cֱ��
�cֱ��![]() �����c(di��n)
�����c(di��n)![]() ����ֱ��
����ֱ��![]() б�ʴ���
б�ʴ���![]() ����ֱ��
����ֱ��![]() ��б��
��б��![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)![]() �քe���p����
�քe���p����![]() �����ҽ��c(di��n)�������p������֧�ϴ����c(di��n)
�����ҽ��c(di��n)�������p������֧�ϴ����c(di��n)![]() ���M��
���M��![]() ����
����![]() ��ֱ��
��ֱ��![]() �ľ��x�����p�����Č�(sh��)�S�L(zh��ng)���tԓ�p�����ĝu�����c���タ
�ľ��x�����p�����Č�(sh��)�S�L(zh��ng)���tԓ�p�����ĝu�����c���タ![]() �Ĝ�(zh��n)�����������ε���e�飨 ��
�Ĝ�(zh��n)�����������ε���e�飨 ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ֱ������(bi��o)ϵ![]() �У���֪�c(di��n)
�У���֪�c(di��n)![]() ��
��![]() ��ֱ��
��ֱ��![]()
![]() ��
��![]() �ֳɃɲ��֣�ӛ���(c��)���ֵĶ�߅�Ξ�
�ֳɃɲ��֣�ӛ���(c��)���ֵĶ�߅�Ξ�![]() .�O(sh��)
.�O(sh��)![]() ��߅�L(zh��ng)��ƽ���͞�
��߅�L(zh��ng)��ƽ���͞�![]() ��
��![]() ��߅�L(zh��ng)�ĵ���(sh��)�͞�
��߅�L(zh��ng)�ĵ���(sh��)�͞�![]() .
.
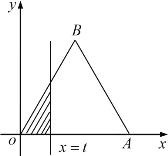
���� �քe��(sh��)![]() ��
��![]() �Ľ���ʽ��
�Ľ���ʽ��
�����Ƿ���څ^(q��)�g![]() ��ʹ�ú���(sh��)
��ʹ�ú���(sh��)![]() ��
��![]() ��ԓ�^(q��)�g�Ͼ����{(di��o)�f�p�������ڣ���
��ԓ�^(q��)�g�Ͼ����{(di��o)�f�p�������ڣ���![]() �����ֵ���������ڣ��f������.
�����ֵ���������ڣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�̈�(ch��ng)����c����(zh��n)���ṩһ�P�Y�𣬌�(du��)���M(f��i)�Mһ�����~����ԅ��c���(d��ng)�ķ�ʽ�M(j��n)�Ъ�(ji��ng)��(l��).͏�һ��(g��)�b�д�С��ͬ��2��(g��)�t���4��(g��)�S��Ĵ��а�ָ��Ҏ(gu��)�tȡ��2��(g��)����(j��)ȡ���ļt��(sh��)�_����(ji��ng)��(l��)���~�����w���~�O(sh��)�����±���
ȡ���ļt��(sh��) | 0 | 1 | 2 |
��(ji��ng)��(l��)����λ��Ԫ�� | 5 | 10 | 50 |
�F(xi��n)�ЃɷNȡ��Ҏ(gu��)�t�ķ�����
����һ��һ�����S�C(j��)ȡ��2��(g��)��
�������������зŻ�ȡ��2��(g��)��.
�����^�ɷN�����£�һ�γ骄(ji��ng)�@��50Ԫ��(ji��ng)����ʵĴ�С��
����ʹ�ñM���ܶ���˅��c���(d��ng)�����鹫˾��ؓ(f��)؟(z��)�����(hu��)�x���ķN������Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������f���e(cu��)�`���ǣ� ��
A.�ڻؚw�����У����P(gu��n)ָ��(sh��)![]() Խ���f������ƽ����ԽС���ؚwЧ��Խ��
Խ���f������ƽ����ԽС���ؚwЧ��Խ��
B.���Իؚw���̌�(du��)��(y��ng)��ֱ��![]() ���ٽ�(j��ng)�^��ӱ���(sh��)��(j��)�c(di��n)�е�һ��(g��)�c(di��n)
���ٽ�(j��ng)�^��ӱ���(sh��)��(j��)�c(di��n)�е�һ��(g��)�c(di��n)
C.�ھ��Իؚw�����У����P(gu��n)ϵ��(sh��)��![]() ��
��![]() Խ�ӽ���1�����P(gu��n)�̶�Խ��
Խ�ӽ���1�����P(gu��n)�̶�Խ��
D.�ڻؚwֱ��![]() �У�׃��
�У�׃��![]() ÿ����һ��(g��)��λ��׃��
ÿ����һ��(g��)��λ��׃��![]() ��s����0.5��(g��)��λ
��s����0.5��(g��)��λ
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]()
��(d��ng)![]() �r(sh��)����(sh��)
�r(sh��)����(sh��)![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��![]() ��D��������һ�c(di��n)
��D��������һ�c(di��n)![]() ̎�о���б��
̎�о���б��![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ��
��![]() �c
�c![]() �ĈD���Ѓɂ�(g��)���c(di��n)
�ĈD���Ѓɂ�(g��)���c(di��n)![]() ,���C��
,���C��![]()
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com