
【題目】已知橢圓![]() 的右焦點與拋物線
的右焦點與拋物線![]() 的焦點重合,且橢圓
的焦點重合,且橢圓![]() 的離心率為
的離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設(shè)![]() 是橢圓
是橢圓![]() 的右頂點,過
的右頂點,過![]() 點作兩條直線分別與橢圓
點作兩條直線分別與橢圓![]() 交于另一點
交于另一點![]() ,若直線
,若直線![]() 的斜率之積為
的斜率之積為![]() ,求證:直線
,求證:直線![]() 恒過一個定點,并求出這個定點的坐標(biāo).
恒過一個定點,并求出這個定點的坐標(biāo).
【答案】(Ⅰ )![]() (Ⅱ)直線
(Ⅱ)直線![]() 恒過點
恒過點![]()
【解析】分析: (Ⅰ)由題意布列關(guān)于a,b的方程組,解之即可;(Ⅱ)設(shè)直線![]() ,與橢圓方程聯(lián)立可得
,與橢圓方程聯(lián)立可得![]() ,利用根與系數(shù)的關(guān)系表示直線
,利用根與系數(shù)的關(guān)系表示直線![]() 的斜率之積為
的斜率之積為![]() ,可得
,可得![]() 值,從而得證.
值,從而得證.
詳解: (Ⅰ)依題意: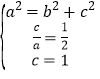 ,解得
,解得![]() ,即橢圓
,即橢圓![]() ;
;
(Ⅱ)設(shè)直線![]() ,
,
則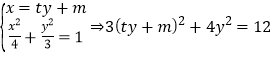 ,
,
即![]() ,
,
![]() ;
;
設(shè)![]() ,而
,而![]() ,則由
,則由![]() 得
得
![]() ,
,
![]() ,
,
即![]() ,
,
整理得![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
![]() 直線
直線![]() ,知直線
,知直線![]() 恒過點
恒過點![]() .
.
點睛: 定點、定值問題通常是通過設(shè)參數(shù)或取特殊值來確定“定點”是什么、“定值”是多少,或者將該問題涉及的幾何式轉(zhuǎn)化為代數(shù)式或三角問題,證明該式是恒定的. 定點、定值問題同證明問題類似,在求定點、定值之前已知該值的結(jié)果,因此求解時應(yīng)設(shè)參數(shù),運用推理,到最后必定參數(shù)統(tǒng)消,定點、定值顯現(xiàn).


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]() 的參數(shù)方程為:
的參數(shù)方程為:![]() (
(![]() 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() .
.
(l)求曲線![]() 和直線
和直線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)已知直線![]() 分別與曲線
分別與曲線![]() 、曲線
、曲線![]() 交異于極點的
交異于極點的![]() ,若
,若![]() 的極徑分別為
的極徑分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)某長產(chǎn)品近幾年的產(chǎn)量統(tǒng)計如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
年產(chǎn)量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若近幾年該農(nóng)產(chǎn)品每千克的價格![]() (單位:元)與年產(chǎn)量
(單位:元)與年產(chǎn)量![]() 滿足的函數(shù)關(guān)系式為
滿足的函數(shù)關(guān)系式為![]() ,且每年該農(nóng)產(chǎn)品都能售完.
,且每年該農(nóng)產(chǎn)品都能售完.
①根據(jù)(1)中所建立的回歸方程預(yù)測該地區(qū)2018(![]() )年該農(nóng)產(chǎn)品的產(chǎn)量;
)年該農(nóng)產(chǎn)品的產(chǎn)量;
②當(dāng)![]() (
(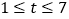 )為何值時,銷售額
)為何值時,銷售額![]() 最大?
最大?
附:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: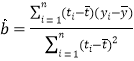 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() 的定義域為
的定義域為![]() ,滿足對任意
,滿足對任意![]() ,有
,有![]() .則稱
.則稱![]() 為“
為“![]() 形函數(shù)”;若函數(shù)
形函數(shù)”;若函數(shù)![]() 定義域為
定義域為![]() ,
,![]() 恒大于0,且對任意
恒大于0,且對任意![]() ,恒有
,恒有![]() ,則稱
,則稱![]() 為“對數(shù)
為“對數(shù)![]() 形函數(shù)”.
形函數(shù)”.
(1)當(dāng)![]() 時,判斷
時,判斷![]() 是否是“
是否是“![]() 形函數(shù)”,并說明理由;
形函數(shù)”,并說明理由;
(2)當(dāng)![]() 時,判斷
時,判斷![]() 是否是“對數(shù)
是否是“對數(shù)![]() 形函數(shù)”,并說明理由;
形函數(shù)”,并說明理由;
(3)若函數(shù)![]() 是
是![]() 形函數(shù),且滿足對任意
形函數(shù),且滿足對任意![]() 都有
都有![]() ,問
,問![]() 是否是“對數(shù)
是否是“對數(shù)![]() 形函數(shù)”?請加以證明,如果不是,請說明理由.
形函數(shù)”?請加以證明,如果不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】秸稈還田是當(dāng)今世界上普通重視的一項培肥地力的增產(chǎn)措施,在杜絕了秸稈焚燒所造成的大氣污染的同時還有增肥增產(chǎn)作用.某農(nóng)機戶為了達(dá)到在收割的同時讓秸稈還田,花![]() 元購買了一臺新型聯(lián)合收割機,每年用于收割可以收入
元購買了一臺新型聯(lián)合收割機,每年用于收割可以收入![]() 萬元(已減去所用柴油費);該收割機每年都要定期進(jìn)行維修保養(yǎng),第一年由廠方免費維修保養(yǎng),第二年及以后由該農(nóng)機戶付費維修保養(yǎng),所付費用
萬元(已減去所用柴油費);該收割機每年都要定期進(jìn)行維修保養(yǎng),第一年由廠方免費維修保養(yǎng),第二年及以后由該農(nóng)機戶付費維修保養(yǎng),所付費用![]() (元)與使用年數(shù)
(元)與使用年數(shù)![]() 的關(guān)系為:
的關(guān)系為:![]() ,已知第二年付費
,已知第二年付費![]() 元,第五年付費
元,第五年付費![]() 元.
元.
(1)試求出該農(nóng)機戶用于維修保養(yǎng)的費用![]() (元)與使用年數(shù)
(元)與使用年數(shù)![]() 的函數(shù)關(guān)系;
的函數(shù)關(guān)系;
(2)這臺收割機使用多少年,可使平均收益最大?(收益=收入-維修保養(yǎng)費用-購買機械費用)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從集合![]() 的所有非空子集中,等可能地取出
的所有非空子集中,等可能地取出![]() 個.
個.
(1)若![]() ,求所取子集的元素既有奇數(shù)又有偶數(shù)的概率;
,求所取子集的元素既有奇數(shù)又有偶數(shù)的概率;
(2)若![]() ,記所取子集的元素個數(shù)之差為
,記所取子集的元素個數(shù)之差為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在國慶![]() 周年慶典活動中,東城區(qū)教育系統(tǒng)近
周年慶典活動中,東城區(qū)教育系統(tǒng)近![]() 名師生參與了國慶中心區(qū)合唱、
名師生參與了國慶中心區(qū)合唱、![]() 方陣群眾游行、聯(lián)歡晚會及
方陣群眾游行、聯(lián)歡晚會及![]() 萬只氣球保障等多項重點任務(wù).設(shè)
萬只氣球保障等多項重點任務(wù).設(shè)![]() 是參與國慶中心區(qū)合唱的學(xué)校
是參與國慶中心區(qū)合唱的學(xué)校![]() ,
,![]() 是參與27方陣群眾游行的學(xué)校
是參與27方陣群眾游行的學(xué)校![]() ,
,![]() 是參與國慶聯(lián)歡晚會的學(xué)校
是參與國慶聯(lián)歡晚會的學(xué)校![]() .請用上述集合之間的運算來表示:①既參與國慶中心區(qū)合唱又參與27方陣群眾游行的學(xué)校的集合為_____;②至少參與國慶中心區(qū)合唱與國慶聯(lián)歡晚會中一項的學(xué)校的集合為_____.
.請用上述集合之間的運算來表示:①既參與國慶中心區(qū)合唱又參與27方陣群眾游行的學(xué)校的集合為_____;②至少參與國慶中心區(qū)合唱與國慶聯(lián)歡晚會中一項的學(xué)校的集合為_____.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com