
���}Ŀ����D�����F![]() �У�
�У�![]() ����Σ�
�����![]() ��
��![]() ��
��![]()
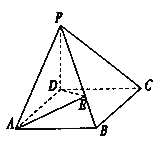
��1����![]() ���Ƿ����һ�c
���Ƿ����һ�c![]() ��ʹ
��ʹ![]() ��
��![]() �������ڴ_��
�������ڴ_��![]() �cλ�ã��������ڣ�Ո�f�����ɣ�
�cλ�ã��������ڣ�Ո�f�����ɣ�
��2����![]() ��
��![]() ���c�r��������
���c�r��������![]() ������ֵ.
������ֵ.
���𰸡���1��Ҋ��������2��![]()
��������
��1��Ҫ�C��PC����ADE������֪�ɵ�AD��PC��ֻ��M��![]() ���ɣ��Ķ��õ��cE�����c;��2�������ADE�ķ���������PAE�ķ����������ÿ��g�����Ĕ�(sh��)���e���������P��AE��D������ֵ��
���ɣ��Ķ��õ��cE�����c;��2�������ADE�ķ���������PAE�ķ����������ÿ��g�����Ĕ�(sh��)���e���������P��AE��D������ֵ��
��1����һ��Ҫ�C��PC����ADE����֪AD����PDC������AD��PC����ֻ��![]() ���ɣ�
���ɣ�
������![]() ,�������cE��PC���c.
,�������cE��PC���c.
������������D��ʾ�Ŀ��gֱ������ϵD��XYZ�� ���}��֪PD��CD��1��
![]() ���O
���O![]() ��
�� ![]() ��
��![]() ����
����
![]() ����
����![]() ��
��
�������cE��PC���c.
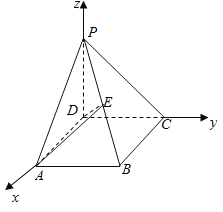
��2���ɣ�1��֪![]() ��
��![]() ��
��![]() ��
��![]()
![]() ��
��![]() ��
�� ![]() ��
��![]()
�O��ADE�ķ�������![]() ����PAE�ķ�������
����PAE�ķ�������![]()
�ɵķ�������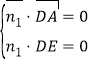 �ã�
�ã� ��
��![]() ��
��
ͬ�����![]()
����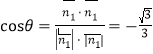 ��
��
����������P��AE��D������ֵ��![]() .
.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ��ij���M����![]() �Δ�(sh��)�W�yԇ�����мס��҃��˵ijɿ��y(t��ng)Ӌ��r���o�~�D��ʾ��
�Δ�(sh��)�W�yԇ�����мס��҃��˵ijɿ��y(t��ng)Ӌ��r���o�~�D��ʾ��
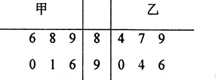
��I��ԓ����(sh��)�W�ώ��Q���ļס��҃������x��һ��ȥ���Ӕ�(sh��)�W��ِ�����J���lȥ�����m�����f�����ɣ�
��II���ļijɿ�����ȥ�ɴ����Mһ���ķ������ڳ�ȡ�ăɴγɿ��У���������һ�γɿ���![]() ֮�g�ĸ���.
֮�g�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
![]() ӑՓ����(sh��)
ӑՓ����(sh��)![]() �Ć��{�ԣ�
�Ć��{�ԣ�
![]() �O
�O![]() ��������
��������![]() ������������(sh��)
�ĺ������������(sh��)![]() �����ֵ��
�����ֵ��
![]() ���C����
���C����![]() �r��
�r��![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ�������{��������Ĕ�(sh��)�W�ɿ��c�W�������W���r�g֮�g�����P�Pϵ�������ЌW��(sh��)�W�̎�������W��![]() ���W���M���˸�ۙ�{�飬����ÿ����������(sh��)�W�}�ĕr�g������
���W���M���˸�ۙ�{�飬����ÿ����������(sh��)�W�}�ĕr�g������![]() С�r����
С�r����![]() �ˣ����µ����У��ڸ���ģ�M��ԇ�Д�(sh��)�W�ɿ�����
�ˣ����µ����У��ڸ���ģ�M��ԇ�Д�(sh��)�W�ɿ�����![]() �ֵ�ռ
�ֵ�ռ![]() ���y(t��ng)Ӌ�ɿ��õ����µ�
���y(t��ng)Ӌ�ɿ��õ����µ�![]() ��(li��n)����
��(li��n)����
�֔�(sh��)���ڵ��� | �֔�(sh��)���� | ��Ӌ | |
�����}�r�g������ | 4 | 19 | |
�����}�r�g���� | |||
��Ӌ | 45 |
��![]() ��Ո��������
��Ո��������![]() ��(li��n)�������Д��ܷ��ڷ��e�`�ĸ��ʲ����^
��(li��n)�������Д��ܷ��ڷ��e�`�ĸ��ʲ����^![]() ��ǰ�����J�顰�������Ĕ�(sh��)�W�ɿ��c�W�������W���r�g���P����
��ǰ�����J�顰�������Ĕ�(sh��)�W�ɿ��c�W�������W���r�g���P����
��![]() ����i�����շӳ�ӵķ������������ӱ��У��ķ֔�(sh��)���ڵ���
����i�����շӳ�ӵķ������������ӱ��У��ķ֔�(sh��)���ڵ���![]() �ֺͷ֔�(sh��)����
�ֺͷ֔�(sh��)����![]() �ֵăɽM�W���г�ȡ
�ֵăɽM�W���г�ȡ![]() ���W�����O�鵽�IJ���
���W�����O�鵽�IJ���![]() ���������}�r�g����
���������}�r�g����![]() С�r���˔�(sh��)��
С�r���˔�(sh��)��![]() ����
����![]() �ķֲ��У������ýM�ϔ�(sh��)��ʽ��ʾ����
�ķֲ��У������ýM�ϔ�(sh��)��ʽ��ʾ����
��ii�����l��ҕ����ʣ���ȫУ���ڵ���![]() �ֵČW�����S�C��ȡ
�ֵČW�����S�C��ȡ![]() �ˣ����@Щ���������}�r�g������
�ˣ����@Щ���������}�r�g������![]() С�r���˔�(sh��)�������ͷ��
С�r���˔�(sh��)�������ͷ��
����![]()
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������
������![]() �c
�c![]() ��ԭ�c̎���о���ͬ��
��ԭ�c̎���о���ͬ��
(1)��![]() ��ֵ��
��ֵ��
(2)��![]() �Ć��{�^(q��)�g�͘Oֵ��
�Ć��{�^(q��)�g�͘Oֵ��
(3)��![]() �r��
�r��![]() ����
����![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
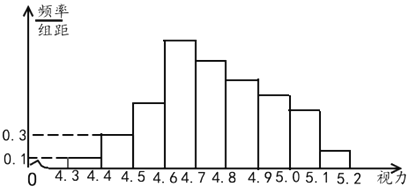
���}Ŀ����D����������100�Ęӱ��õ����l�ʷֲ�ֱ���D������ǰ4�M���l�ʳɵȱȔ�(sh��)�У���6�M���l��(sh��)�ɵȲ(sh��)�У��O����l�ʞ�a����![]() ��
��![]() ֮�g�Ĕ�(sh��)��(j��)����(sh��)��b���ta��b��ֵ�քe�飨 ��
֮�g�Ĕ�(sh��)��(j��)����(sh��)��b���ta��b��ֵ�քe�飨 ��
A.![]() ��78
��78
B.![]() ��83
��83
C.![]() ��78
��78
D.![]() ��83
��83
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������ϵ��ԭ�c��O�c��![]() �S�������S��O�S�������O����ϵ����ֱ֪��
�S�������S��O�S�������O����ϵ����ֱ֪��![]() �ą���(sh��)������
�ą���(sh��)������ (m>0,t�酢��(sh��))������
(m>0,t�酢��(sh��))������![]() �ĘO���˷��̞�
�ĘO���˷��̞�![]() ��
��
��1����ֱ��![]() ����ͨ���̺�����
����ͨ���̺�����![]() ��ֱ�����˷��̣�
��ֱ�����˷��̣�
��2����ֱ��![]() �c
�c![]() �S�����c
�S�����c![]() ���c����
���c����![]() �����c
�����c![]() ����
����![]() ����(sh��)
����(sh��)![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
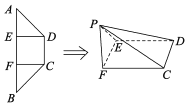
���}Ŀ����D��ʾ���ڵ�������ABCD�У�![]() ��
��![]() ��E��F��AB�����ȷ��c����
��E��F��AB�����ȷ��c����![]() ��
��![]() ��
��![]() �քe��DE��CF����A��B���c�غϣ�ӛ���cP��
�քe��DE��CF����A��B���c�غϣ�ӛ���cP��
![]() �C����ƽ��
�C����ƽ��![]() ƽ��PEF��
ƽ��PEF��
![]() ��
��![]() ����PD�cƽ��PFC���ɽǵ�����ֵ��
����PD�cƽ��PFC���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ������܇�˷���!��3000Ԫ���_��܇���@����ë����܇�W������ďV���Z��ij�˿����V�棬�d�^���ѣ�Ӌ����2019��1����ԓ�Wվُ�Iһ�vijƷ����܇�����Į�?sh��)��˽���傀��ԓƷ����܇���H�N�������
�·� | 2018.08 | 2018.09 | 2018.10 | 2018.11 | 2018.12 |
�·ݾ�̖t | 1 | 2 | 3 | 4 | 5 |
�N��y���f�v�� | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
��1�������������þ��Իؚwģ�͔M�Ϯ�?sh��)�ԓƷ����܇���H�N��y���f�v���c�·ݾ�̖t֮�g�����P�Pϵ��Ո����С���˷���y�P��t�ľ��Իؚw����![]() ������Ӌ2019��1�·�ԓƷ����܇���N����
������Ӌ2019��1�·�ԓƷ����܇���N����
��2�����������N�����S�Һ�ë����܇�W(li��n)���Ƴ���ُԓƷ��܇�M���a�N����֪ij�ؔMُ�IԓƷ����܇�����MȺ�wʮ������ij�{�ЙC�������е�200�����M�ߵ�ُ܇�a�N���~�������A��ֵ�M����һ������{�飬�õ�����һ���l��(sh��)����
�a�N���~�A��ֵ �^(q��)�g���fԪ�� | [1��2�� | [2��3�� | [3��4�� | [4��5�� | [5��6�� | [6��7�� |
�l��(sh��) | 20 | 60 | 60 | 30 | 20 | 10 |
���l��ҕ����ʣ��F(xi��n)���S�C��ӷ�����ԓ�^(q��)�Mُ�IԓƷ����܇���������M�����S�C��ȡ3�ˣ�ӛ����ȡ3���Ќ��a�N���~�������A��ֵ������3�fԪ���˔�(sh��)�����������ķֲ��м���(sh��)�W����E������
������ʽ����(sh��)��(j��)���ٻؚw����![]() ������
������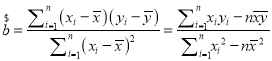 ��
��![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
���H�WУ��(y��u)�x - �������б� - ԇ�}�б�
����ʡ��(li��n)�W�`���Ͳ�����Ϣ�e��ƽ�_ | �W���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙��e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com