
【題目】已知橢圓C: ![]() 的離心率為
的離心率為![]() ,右焦點為F,上頂點為A,且△AOF的面積為
,右焦點為F,上頂點為A,且△AOF的面積為![]() (O為坐標原點).
(O為坐標原點).
(1)求橢圓C的方程;
(2)設P是橢圓C上的一點,過P的直線與以橢圓的短軸為直徑的圓切于第一象限內的一點M,證明:|PF|+|PM|為定值.
【答案】(1) ![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】試題分析:(1)根據橢圓的幾何性質得到a=![]() c,bc=1,解得方程;(2)設橢圓上一點為.P(
c,bc=1,解得方程;(2)設橢圓上一點為.P(![]() cos θ,sin θ),用點點距離表示|PF|+|PM|,最終求得定值。
cos θ,sin θ),用點點距離表示|PF|+|PM|,最終求得定值。
解析:
(1)解 由題意可知:橢圓的離心率e=![]() ,則a=
,則a=![]() c.
c.
由△AOF的面積為S=![]() ×b×c=
×b×c=![]() ,則bc=1,
,則bc=1,
由a2=b2+c2,解得a=![]() ,b=c=1.
,b=c=1.
∴橢圓的標準方程為![]() ;.
;.
(2)證明 由(1)知:F(1,0),以橢圓的短軸為直徑的圓的方程為x2+y2=1,
設P(![]() cos θ,sin θ),且cos θ>0,
cos θ,sin θ),且cos θ>0,
則|PF|=![]() =
=
由M是圓x2+y2=1的切點,則OM⊥PM,且|OM|=1,
則|PM|=![]() =cos θ,
=cos θ,
∴|PF|+|PM|=![]() -cos θ+cos θ=
-cos θ+cos θ=![]() ,
,
∴|PF|+|PM|為定值.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】在統計學中,偏差是指個別測定值與測定的平均值之差,在成績統計中,我們把某個同學的某科考試成績與該科班平均分的差叫某科偏差,班主任為了了解個別學生的偏科情況,對學生數學偏差x(單位:分)與物理偏差y(單位:分)之間的關系進行學科偏差分析,決定從全班56位同學中隨機抽取一個容量為8的樣本進行分析,得到他們的兩科成績偏差數據如下:
學生序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
數學偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x與y之間具有線性相關關系,求y關于x的線性回歸方程;
(2)若這次考試該班數學平均分為118分,物理平均分為90.5,試預測數學成績126分的同學的物理成績.
參考公式: 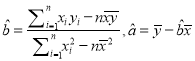 .
.
參考數據: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;(Ⅱ)若c=![]() ,△ABC的面積為
,△ABC的面積為![]() ,求△ABC的周長.
,求△ABC的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·河西五市二聯)下列說法正確的是( )
A. 命題“x∈R,ex>0”的否定是“x∈R,ex>0”
B. 命題“已知x,y∈R,若x+y≠3,則x≠2或y≠1”是真命題
C. “x2+2x≥ax在x∈[1,2]上恒成立”“(x2+2x)min≥(ax)min在x∈[1,2]上恒成立”
D. 命題“若a=-1,則函數f(x)=ax2+2x-1只有一個零點”的逆命題為真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
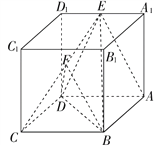
【題目】如圖,正方體ABCD-A1B1C1D1中,點E是A1D1的中點,點F是CE的中點.
(Ⅰ)求證:平面ACE⊥平面BDD1B1;
(Ⅱ)求證:AE∥平面BDF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是遞增的等比數列,滿足
是遞增的等比數列,滿足![]() ,且
,且![]() 是
是![]() 、
、![]() 的等差中項,數列
的等差中項,數列![]() 滿足
滿足![]() ,其前
,其前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求數列![]() ,
,![]() 的通項公式;
的通項公式;
(2)數列![]() 的前
的前![]() 項和為
項和為![]() ,若不等式
,若不等式![]() 對一切
對一切![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
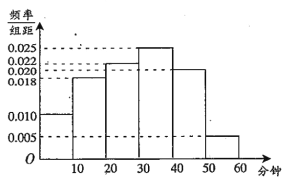
【題目】某中學為研究學生的身體素質與課外體育鍛煉時間的關系,對該校200名學生的課外體育鍛煉平均每天運動的時間(單位:分鐘)進行調查,將收集的數據分成![]() 六組,并作出頻率分布直方圖(如圖),將日均課外體育鍛煉時間不低于40分鐘的學生評價為“課外體育達標”.
六組,并作出頻率分布直方圖(如圖),將日均課外體育鍛煉時間不低于40分鐘的學生評價為“課外體育達標”.
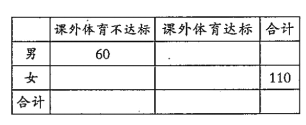
(1)請根據直方圖中的數據填寫下面的![]() 列聯表,并通過計算判斷是否能在犯錯誤的概率不超過0.01的前提下認為“課外體育達標”與性別有關?
列聯表,并通過計算判斷是否能在犯錯誤的概率不超過0.01的前提下認為“課外體育達標”與性別有關?
(2)在[0,10),[40,50)這兩組中采取分層抽樣,抽取6人,再從這6名學生中隨機抽取2人參加體育知識問卷調查,求這2人中一人來自“課外體育達標”和一人來自“課外體育不達標”的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(導學號:05856335)[選修4-4:坐標系與參數方程]
以原點為極點,x軸的非負半軸為極軸建立極坐標系.已知A(2,π),B(2, ![]() ),圓C的極坐標方程為ρ2-6ρcos θ+8ρsin θ+21=0.F為圓C上的任意一點.
),圓C的極坐標方程為ρ2-6ρcos θ+8ρsin θ+21=0.F為圓C上的任意一點.
(Ⅰ)寫出圓C的參數方程;
(Ⅱ)求△ABF的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com