
【題目】已知函數f(x)=x2+ax+b﹣a(a,b∈R).
(1)若關于x的不等式f(x)>0的解集為(﹣∞,﹣1)∪(3,+∞),求實數a,b的值;
(2)設a=2,若不等式f(x)>b2﹣3b對任意實數x都成立,求實數b的取值范圍;
(3)設b=3,解關于x的不等式組 ![]() .
.
【答案】
(1)解:因為不等式f(x)=x2+ax+b﹣a>0的解集為(﹣∞,﹣1)∪(3,+∞),
所以由題意得﹣1,3為函數x2+ax+b﹣a=0的兩個根,
所以 ![]() ,解得a=﹣2,b=﹣5
,解得a=﹣2,b=﹣5
(2)解:當a=2時,x2+2x+b﹣2>b2﹣3b恒成立,即x2+2x﹣2>b2﹣4b恒成立.
因為x2+2x﹣2=(x+1)2﹣3≥﹣3,所以b2﹣4b<﹣3,
解之得1<b<3,所以實數b的取值范圍為1<b<3
(3)當b=3時,f(x)=x2+ax+3﹣a,f(x)的圖象的對稱軸為 ![]() .
.
(ⅰ)當△<0,即﹣6<a<2時,由 ![]() ,得x>1,
,得x>1,
(ⅱ)當△=0,即a=2或﹣6時
①當a=2時,由 ![]() ,得
,得 ![]() ,所以x>1,
,所以x>1,
②當a=﹣6時,由 ![]() ,得
,得 ![]() ,所以1<x<3或x>3,
,所以1<x<3或x>3,
(ⅲ)當△>0,即a<﹣6或a>2時,方程f(x)=0的兩個根為 ![]() ,
, ![]() ,
,
①當a<﹣6時,由 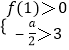 知1<x1<x2,所以
知1<x1<x2,所以 ![]() 的解為1<x<x1或x>x2,
的解為1<x<x1或x>x2,
②當a>2時,由 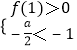 知x1<x2<1,所以
知x1<x2<1,所以 ![]() 的解為x>1,
的解為x>1,
綜上所述,
當a≤﹣6時,不等式組的解集為 ![]() ,
,
當a>﹣6時,不等式組的解集為(1,+∞)
【解析】(1)把問題轉化為一元二次方程的問題,利用方程的根建立二次一次方程組,求得a和b的值.(2)把不等式整理成x2+2x﹣2>b2﹣4b確定等號左邊的最小值,進而確定等號右邊的范圍求得b的范圍.(3)對判別式△大于0和小于0進行分類討論,通過解不等式求得解集.
【考點精析】認真審題,首先需要了解二次函數的性質(當![]() 時,拋物線開口向上,函數在
時,拋物線開口向上,函數在![]() 上遞減,在
上遞減,在![]() 上遞增;當
上遞增;當![]() 時,拋物線開口向下,函數在
時,拋物線開口向下,函數在![]() 上遞增,在
上遞增,在![]() 上遞減).
上遞減).


科目:高中數學 來源: 題型:
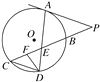
【題目】如圖所示,已知PA與⊙O相切,A為切點,PBC為割線,弦CD∥AP,AD,BC相交于E點,F為CE上一點,且DE2=EF·EC.
(1)求證:∠P=∠EDF;
(2)求證:CE·EB=EF·EP;
(3)若CE∶BE=3∶2,DE=6,EF=4,求PA的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+φ) ![]() 的最小正周期為π,
的最小正周期為π,
(1)求當f(x)為偶函數時φ的值;
(2)若f(x)的圖象過點( ![]() ,
, ![]() ),求f(x)的單調遞增區間.
),求f(x)的單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知角α的頂點在坐標原點,始邊與x軸的非負半軸重合,終邊經過點 ![]() .
.
(1)求sin2α﹣tanα的值;
(2)若函數f(x)=cos(x﹣α)cosα﹣sin(x﹣α)sinα,求函數 ![]() 在區間
在區間 ![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=x3﹣2ex2+mx﹣lnx,記g(x)= ![]() ,若函數g(x)至少存在一個零點,則實數m的取值范圍是( )
,若函數g(x)至少存在一個零點,則實數m的取值范圍是( )
A.(﹣∞,e2+ ![]() ]
]
B.(0,e2+ ![]() ]
]
C.(e2+ ![]() ,+∞]
,+∞]
D.(﹣e2﹣ ![]() ,e2+
,e2+ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個四棱錐的三視圖如圖所示,關于這個四棱錐,下列說法正確的是( )

A. 最長的棱長為![]()
B. 該四棱錐的體積為![]()
C. 側面四個三角形都是直角三角形
D. 側面三角形中有且僅有一個等腰三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com