
【題目】過年時小明的舅舅在家庭微信群里發了一個10元的紅包,紅包被隨機分配為2.51元,3.32元,1.24元,0.26元,2.67元,共五份.現已知小明與爸爸都各自搶到了一個紅包,則兩人搶到紅包的金額總和不小于4元的概率為__________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】過去大多數人采用儲蓄的方式將錢儲蓄起來,以保證自己生活的穩定,考慮到通貨膨脹的壓力,如果我們把所有的錢都用來儲蓄,這并不是一種很好的方式,隨著金融業的發展,普通人能夠使用的投資理財工具也多了起來,為了研究某種理財工具的使用情況,現對![]() 年齡段的人員進行了調查研究,將各年齡段人數分成
年齡段的人員進行了調查研究,將各年齡段人數分成![]() 組:
組:![]() ,并整理得到頻率分布直方圖:
,并整理得到頻率分布直方圖:
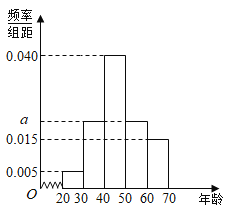
(1)求圖中的![]() 值;
值;
(2)采用分層抽樣的方法,從第二組、第三組、第四組中共抽取![]() 人,則三個組中各抽取多少人?
人,則三個組中各抽取多少人?
(3)在(2)中抽取的![]() 人中,隨機抽取
人中,隨機抽取![]() 人,則這
人,則這![]() 人都來自于第三組的概率是多少?
人都來自于第三組的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的長軸長是短軸長的2倍,且過點
的長軸長是短軸長的2倍,且過點![]() .
.
⑴求橢圓![]() 的方程;
的方程;
⑵若在橢圓上有相異的兩點![]() (
(![]() 三點不共線),
三點不共線),![]() 為坐標原點,且直線
為坐標原點,且直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率滿足
的斜率滿足![]() .
.
(ⅰ)求證: ![]() 是定值;
是定值;
(ⅱ)設![]() 的面積為
的面積為![]() ,當
,當![]() 取得最大值時,求直線
取得最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是離心率為
是離心率為![]() 的橢圓
的橢圓![]()
![]() 兩焦點,若存在直線
兩焦點,若存在直線![]() ,使得
,使得![]() ,
,![]() 關于
關于![]() 的對稱點的連線恰好是圓
的對稱點的連線恰好是圓![]()
![]() 的一條直徑.
的一條直徑.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的上頂點
的上頂點![]() 作斜率為
作斜率為![]() ,
,![]() 的兩條直線
的兩條直線![]() ,
,![]() ,兩直線分別與橢圓交于
,兩直線分別與橢圓交于![]() ,
,![]() 兩點,當
兩點,當![]() 時,直線
時,直線![]() 是否過定點?若是求出該定點,若不是請說明理由.
是否過定點?若是求出該定點,若不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() 是以坐標原點
是以坐標原點![]() 為頂點,直線
為頂點,直線![]() 為準線的拋物線.以坐標原點
為準線的拋物線.以坐標原點![]() 為極點,
為極點,![]() 軸非負半軸為極軸建立極坐標系.
軸非負半軸為極軸建立極坐標系.
(1)分別求出直線![]() 與曲線
與曲線![]() 的極坐標方程:
的極坐標方程:
(2)點![]() 是曲線
是曲線![]() 上位于第一象限內的一個動點,點
上位于第一象限內的一個動點,點![]() 是直線
是直線![]() 上位于第二象限內的一個動點,且
上位于第二象限內的一個動點,且![]() ,請求出
,請求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() ,
,![]() ,
,![]() 分別是橢圓短軸的上下兩個端點,
分別是橢圓短軸的上下兩個端點,![]() 是橢圓的左焦點,P是橢圓上異于點
是橢圓的左焦點,P是橢圓上異于點![]() ,
,![]() 的點,若
的點,若![]() 的邊長為4的等邊三角形.
的邊長為4的等邊三角形.
![]() 寫出橢圓的標準方程;
寫出橢圓的標準方程;
![]() 當直線
當直線![]() 的一個方向向量是
的一個方向向量是![]() 時,求以
時,求以![]() 為直徑的圓的標準方程;
為直徑的圓的標準方程;
![]() 設點R滿足:
設點R滿足:![]() ,
,![]() ,求證:
,求證:![]() 與
與![]() 的面積之比為定值.
的面積之比為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知曲線 (
(![]() 為參數),
為參數),![]() .以原點
.以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(I)寫出曲線![]() 與圓
與圓![]() 的極坐標方程;
的極坐標方程;
(II)在極坐標系中,已知射線![]() 分別與曲線
分別與曲線![]() 及圓
及圓![]() 相交于
相交于![]() ,當
,當![]() 時,求
時,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]()
![]() 的焦點為
的焦點為![]() ,直線
,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,與拋物線
,與拋物線![]() 的交點為
的交點為![]() ,且
,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)過拋物線![]() 上一點
上一點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() 和
和![]() ,試問直線
,試問直線![]() 是否過定點,若是,求出該定點;若不是,請說明理由.
是否過定點,若是,求出該定點;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com