Question

【題目】已知函數f（x）＝ax3＋bx2＋cx在x＝±1處取得極值，在x＝0處的切線與直線3x＋y＝0平行．

（1）求f（x）的解析式；

（2）已知點A（2，m），求過點A的曲線y＝f（x）的切線條數．

Answer 1

【答案】（1）f（x）＝x3－3x；（2）①當m>2或m<－6時，方程m＝－2t3＋6t2－6只有一解，即過點A只有一條切線；②當m＝2或m＝－6時，方程m＝－2t3＋6t2－6恰有兩解，即過點A有兩條切線；③當－6<m<2時，方程m＝－2t3＋6t2－6有三解，即過點A有三條切線．

【解析】

試題分析：（1）求導，利用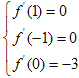進行求解；（2）設出切點坐標，利用導數的幾何意義求其斜率，寫出切線方程，構造函數，利用導數研究極值，再通過數形結合思想求解．

試題解析：（1）f′（x）＝3ax2＋2bx＋c，

由題意可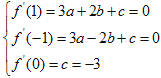得解得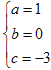所以f（x）＝x3－3x．

（2）設切點為（t，t3－3t），由（1）知f′（x）＝3x2－3，所以切線斜率k＝3t2－3，

切線方程為y－（t3－3t）＝（3t2－3）（x－t）．

又切線過點A（2，m），代入得m－（t3－3t）＝（3t2－3）（2－t），解得m＝－2t3＋6t2－6．

設g（t）＝－2t3＋6t2－6，令g′（t）＝0，即－6t2＋12t＝0，解得t＝0或t＝2．

當t變化時，g′（t）與g（t）的變化情況如下表：

t	（－∞，0）	0	（0,2）	2	（2，＋∞）
g′（t）	－	0	＋	0	－
g（t）	↘	極小值	↗	極大值	↘

所以g（t）的極小值為g（0）＝－6，極大值為g（2）＝2．

p>作出函數草圖可知：

①當m>2或m<－6時，方程m＝－2t3＋6t2－6只有一解，即過點A只有一條切線；

②當m＝2或m＝－6時，方程m＝－2t3＋6t2－6恰有兩解，即過點A有兩條切線；

③當－6<m<2時，方程m＝－2t3＋6t2－6有三解，即過點A有三條切線．