
【題目】已知函數(shù)![]() ,
,![]() ,若對任意給定的
,若對任意給定的![]() ,關(guān)于
,關(guān)于![]() 的方程
的方程![]() 在區(qū)間
在區(qū)間![]() 上總存在唯一的一個解,則實數(shù)
上總存在唯一的一個解,則實數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:由題意可以把問題轉(zhuǎn)化為求函數(shù)f(x)和函數(shù)g(x)的值域,并有題意轉(zhuǎn)化為兩個函數(shù)的值域的關(guān)系問題.
詳解:解f′(x)=6ax2﹣6ax=6ax(x﹣1),
①當a=0時,f(x)=1,g(x)=![]() ,顯然不可能滿足題意;
,顯然不可能滿足題意;
②當a>0時,f'(x)=6ax2﹣6ax=6ax(x﹣1),
x,f′(x),f(x)的變化如下:

又因為當a>0時,g(x)=﹣![]() x+
x+![]() 上是減函數(shù),
上是減函數(shù),
對任意m∈[0,2],g(m)∈[﹣![]() +
+![]() ,
,![]() ],
],
由題意,必有g(m)max≤f(x)max,且1﹣a>0,
故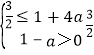 ,解得:
,解得:![]() ≤a<1,
≤a<1,
③當a<0時,g(x)=﹣![]() x+
x+![]() 上是增函數(shù),不合題意;
上是增函數(shù),不合題意;
綜上,a∈[![]() ,1),
,1),
故選:B.


科目:高中數(shù)學 來源: 題型:
【題目】某地區(qū)某農(nóng)產(chǎn)品近五年的產(chǎn)量統(tǒng)計如下表:

(Ⅰ)根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ,并由所建立的回歸方程預測該地區(qū)2018年該農(nóng)產(chǎn)品的產(chǎn)量;
,并由所建立的回歸方程預測該地區(qū)2018年該農(nóng)產(chǎn)品的產(chǎn)量;
(Ⅱ)若近五年該農(nóng)產(chǎn)品每千克的價格![]() (單位:元)與年產(chǎn)量
(單位:元)與年產(chǎn)量![]() (單位:萬噸)滿足的函數(shù)關(guān)系式為
(單位:萬噸)滿足的函數(shù)關(guān)系式為![]() ,且每年該農(nóng)產(chǎn)品都能售完.求年銷售額
,且每年該農(nóng)產(chǎn)品都能售完.求年銷售額![]() 最大時相應的年份代碼
最大時相應的年份代碼![]() 的值,
的值,
附:對于一組數(shù)據(jù)![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的計算公式:
的斜率和截距的計算公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知定義域為![]() 的函數(shù)
的函數(shù)![]() 是奇函數(shù).
是奇函數(shù).
(1)求![]() 的值;
的值;
(2)判斷函數(shù)![]() 在
在![]() 上的單調(diào)性,并證明你的結(jié)論.
上的單調(diào)性,并證明你的結(jié)論.
(3)是否存在實數(shù)![]() ,對于任意
,對于任意![]() ,不等式
,不等式![]() 恒成立,若存在,求出實數(shù)
恒成立,若存在,求出實數(shù)![]() 的取值范圍,若不存在,說明理由.
的取值范圍,若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() .
.
(1)當![]() 時,若對任意
時,若對任意![]() 均有
均有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設直線![]() 與曲線
與曲線![]() 和曲線
和曲線![]() 相切,切點分別為
相切,切點分別為![]() ,
,![]() ,其中
,其中![]() .
.
①求證:![]() ;
;
②當![]() 時,關(guān)于
時,關(guān)于![]() 的不等式
的不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數(shù)方程為
,其參數(shù)方程為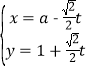 (
(![]() 為參數(shù),
為參數(shù),![]() ),以坐標原點為極點,以
),以坐標原點為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點(
兩點(![]() 在
在![]() 之間),且
之間),且![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題正確的有________(只填序號)
①若直線與平面有無數(shù)個公共點,則直線在平面內(nèi);
②若直線l上有無數(shù)個點不在平面α內(nèi),則l∥α;
③若兩條異面直線中的一條與一個平面平行,則另一條直線一定與該平面相交;
④若直線l與平面α平行,則l與平面α內(nèi)的直線平行或異面;
⑤若平面α∥平面β,直線aα,直線bβ,則直線a∥b.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2018年2月22日,在韓國平昌冬奧會短道速滑男子![]() 米比賽中,中國選手武大靖以連續(xù)打破世界紀錄的優(yōu)異表現(xiàn),為中國代表隊奪得了本屆冬奧會的首枚金牌,也創(chuàng)造了中國男子冰上競速項目在冬奧會金牌零的突破.根據(jù)短道速滑男子
米比賽中,中國選手武大靖以連續(xù)打破世界紀錄的優(yōu)異表現(xiàn),為中國代表隊奪得了本屆冬奧會的首枚金牌,也創(chuàng)造了中國男子冰上競速項目在冬奧會金牌零的突破.根據(jù)短道速滑男子![]() 米的比賽規(guī)則,運動員自出發(fā)點出發(fā)進入滑行階段后,每滑行一圈都要依次經(jīng)過
米的比賽規(guī)則,運動員自出發(fā)點出發(fā)進入滑行階段后,每滑行一圈都要依次經(jīng)過![]() 個直道與彎道的交接口
個直道與彎道的交接口![]() .已知某男子速滑運動員順利通過每個交接口的概率均為
.已知某男子速滑運動員順利通過每個交接口的概率均為![]() ,摔倒的概率均為
,摔倒的概率均為![]() .假定運動員只有在摔倒或到達終點時才停止滑行,現(xiàn)在用
.假定運動員只有在摔倒或到達終點時才停止滑行,現(xiàn)在用![]() 表示該運動員滑行最后一圈時在這一圈內(nèi)已經(jīng)順利通過的交接口數(shù).
表示該運動員滑行最后一圈時在這一圈內(nèi)已經(jīng)順利通過的交接口數(shù).
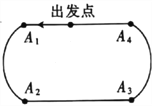
(1)求該運動員停止滑行時恰好已順利通過![]() 個交接口的概率;
個交接口的概率;
(2)求![]() 的分布列及數(shù)學期望
的分布列及數(shù)學期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,且
是菱形,且![]() .點
.點
![]() 是棱
是棱![]() 的中點,平面
的中點,平面![]() 與棱
與棱![]() 交于點
交于點![]() .
.

(1)求證:![]() ∥
∥![]() ;
;
(2)若![]() ,且平面
,且平面![]() 平面
平面![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com