
【題目】設數列![]() 是首項為0的遞增數列,
是首項為0的遞增數列,![]() ,滿足:對于任意的
,滿足:對于任意的![]() 總有兩個不同的根,則
總有兩個不同的根,則![]() 的通項公式為_________
的通項公式為_________
【答案】![]()
【解析】
試題分析:∵![]() ,當n=1時,f1(x)=|sin(x-a1)|=|sinx|,x∈[0,a2],
,當n=1時,f1(x)=|sin(x-a1)|=|sinx|,x∈[0,a2],
又∵對任意的b∈[0,1),f1(x)=b總有兩個不同的根,∴a2=π
∴f1(x)=sinx,x∈[0,π],a2=π
又f2(x)=|sin ![]() (x-a2)|=|sin
(x-a2)|=|sin ![]() (x-π)|=|cos
(x-π)|=|cos ![]() |,x∈[π,a3]
|,x∈[π,a3]
∵對任意的b∈[0,1),f1(x)=b總有兩個不同的根,∴![]() …(5分)
…(5分)
又f3(x)=|sin ![]() (x-a3)|=|sin
(x-a3)|=|sin ![]() (x-3π)|=|sin
(x-3π)|=|sin ![]() π|,x∈[3π,a4]
π|,x∈[3π,a4]
∵對任意的b∈[0,1),f1(x)=b總有兩個不同的根,∴a4=6π…(6分)
由此可得![]() ,
,
∴![]()
∴![]()


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有兩個不同的解
上有兩個不同的解![]() .
.
(ⅰ)求![]() 的取值范圍;
的取值范圍;
(ⅱ)若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)設函數![]() 在區間
在區間![]() 上的最大值和最小值分別為
上的最大值和最小值分別為![]() ,求
,求![]() 的表達式.
的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某地參加2015 年夏令營的![]() 名學生的身體健康情況,將學生編號為
名學生的身體健康情況,將學生編號為![]() ,采用系統抽樣的方法抽取一個容量為
,采用系統抽樣的方法抽取一個容量為![]() 的樣本,且抽到的最小號碼為
的樣本,且抽到的最小號碼為![]() ,已知這
,已知這![]() 名學生分住在三個營區,從
名學生分住在三個營區,從![]() 到
到![]() 在第一營區,從
在第一營區,從![]() 到
到![]() 在第二營區,從
在第二營區,從![]() 到
到![]() 在第三營區,則第一、第二、第三營區被抽中的人數分別為( )
在第三營區,則第一、第二、第三營區被抽中的人數分別為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方體![]() 的棱長為1,
的棱長為1,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點,過直線
的中點,過直線![]() 的平面分別與棱
的平面分別與棱![]() 、
、![]() 交于
交于![]() ,設
,設![]() ,
,![]() ,給出以下四個命題:
,給出以下四個命題:
①四邊形![]() 為平行四邊形;
為平行四邊形;
②若四邊形![]() 面積
面積![]() ,
,![]() ,則
,則![]() 有最小值;
有最小值;
③若四棱錐![]() 的體積
的體積![]()
![]() ,
,![]() ,則
,則![]() 為常函數;
為常函數;
④若多面體![]() 的體積
的體積![]() ,
,![]() ,則
,則![]() 為單調函數.
為單調函數.
其中假命題為( )
A.① ③ B.② C.③④ D.④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C經過點A(﹣2,0),B(0,2),且圓心C在直線y=x上,又直線l:y=kx+1與圓C相交于P、Q兩點.
(1)求圓C的方程;
(2)若![]()
![]() =﹣2,求實數k的值;
=﹣2,求實數k的值;
(3)過點(0,4)作動直線m交圓C于E,F兩點.試問:在以EF為直徑的所有圓中,是否存在這樣的圓P,使得圓P經過點M(2,0)?若存在,求出圓P的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在銳角△ABC中,兩向量p=(2-2sin A,cos A+sin A),q=(sin A-cos A,1+sin A),且p與q是共線向量.
(1)求A的大小;
(2)求函數y=2sin2B+cos(![]() )取最大值時,角B的大小.
)取最大值時,角B的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在坐標原點![]() 的橢圓
的橢圓![]() 經過點
經過點![]() ,且點
,且點![]() 為其右焦點.
為其右焦點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)是否存在平行于![]() 的直線
的直線![]() ,使得直線
,使得直線![]() 與橢圓
與橢圓![]() 有公共點,且直線
有公共點,且直線![]() 與
與![]() 的距離等于4?若存在,求出直線
的距離等于4?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】水培植物需要一種植物專用營養液.已知每投放![]() (
(![]() 且
且![]() )個單位的營養液,它在水中釋放的濃度
)個單位的營養液,它在水中釋放的濃度![]() (克/升)隨著時間
(克/升)隨著時間![]() (天)變化的函數關系式近似為
(天)變化的函數關系式近似為![]() ,其中
,其中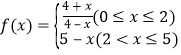 ,若多次投放,則某一時刻水中的營養液濃度為每次投放的營養液在相應時刻所釋放的濃度之和,根據經驗,當水中營養液的濃度不低于4(克/升)時,它才能有效.
,若多次投放,則某一時刻水中的營養液濃度為每次投放的營養液在相應時刻所釋放的濃度之和,根據經驗,當水中營養液的濃度不低于4(克/升)時,它才能有效.
(1)若只投放一次4個單位的營養液,則有效時間可能達幾天?
(2)若先投放2個單位的營養液,3天后投放![]() 個單位的營養液.要使接下來的2天中,營養液能夠持續有效,試求
個單位的營養液.要使接下來的2天中,營養液能夠持續有效,試求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com