
���}Ŀ����֪�E�AC: ![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ���x����
���x����![]() ��
��
��1����E�AC�Ę�(bi��o)��(zh��n)���̣�
��2����֪?ji��ng)�ֱ��l�^�c(di��n)F�����c�E�AC����A��B���c(di��n)��ԇ��x�S���Ƿ���ڶ��c(di��n)M ��ʹ��![]() ������������ڣ�����c(di��n)M������(bi��o)���������ڣ�Ո(q��ng)�f�����ɣ�
������������ڣ�����c(di��n)M������(bi��o)���������ڣ�Ո(q��ng)�f�����ɣ�
���𰸡���1��![]() ��
��
��2��x�S�ϴ����c(di��n)![]() ��ʹ��
��ʹ��![]() �����������Ҋ����.
�����������Ҋ����.
��������
��1������(j��)���c(di��n)����(bi��o)���x���ʽY(ji��)��![]() ��ʽ�����
��ʽ�����![]() ��ֵ���Ķ���ÙE�A�Ę�(bi��o)��(zh��n)����.
��ֵ���Ķ���ÙE�A�Ę�(bi��o)��(zh��n)����.
��2�����O(sh��)![]() �S�ϴ���
�S�ϴ���![]() ��ʹ
��ʹ![]() .��(d��ng)ֱ��
.��(d��ng)ֱ��![]() б�ʞ�
б�ʞ�![]() �r(sh��)�����
�r(sh��)�����![]() ���c(di��n)������(bi��o)������
���c(di��n)������(bi��o)������![]() �з��̣��ⷽ�����
�з��̣��ⷽ�����![]() ��ֵ.��(d��ng)ֱ��
��ֵ.��(d��ng)ֱ��![]() б�ʲ����ڕr(sh��)�����
б�ʲ����ڕr(sh��)�����![]() ���c(di��n)������(bi��o)������
���c(di��n)������(bi��o)������![]() �з��̣��ⷽ�����
�з��̣��ⷽ�����![]() ��ֵ.�ɴ��Д�
��ֵ.�ɴ��Д�![]() ���ɴ����
���ɴ����![]() �c(di��n)����(bi��o)�����C��(d��ng)ֱ��
�c(di��n)����(bi��o)�����C��(d��ng)ֱ��![]() б�ʴ��ڕr(sh��)��
б�ʴ��ڕr(sh��)��![]() ����.��(d��ng)ֱ��
����.��(d��ng)ֱ��![]() б�ʴ��ڕr(sh��)���O(sh��)��ֱ��
б�ʴ��ڕr(sh��)���O(sh��)��ֱ��![]() �ķ��̣�(li��n)��ֱ�����̺͙E�A���̣������f�_(d��)������Ӌ(j��)���
�ķ��̣�(li��n)��ֱ�����̺͙E�A���̣������f�_(d��)������Ӌ(j��)���![]() ���ɴ���÷����}���
���ɴ���÷����}���![]() �c(di��n)������(bi��o).
�c(di��n)������(bi��o).
��1���� ![]() ��
��![]() �� ��
�� ��![]() ��
��
�� ![]() ��
��
�� �E�A���̞�![]() ��
��
��2�����O(sh��)x�S�ϴ����c(di��n)M(m,0),ʹ��![]() ,
,
�ٮ�(d��ng)ֱ��l��б�ʞ�0�r(sh��), ![]() ,
,![]() ,
,
�t![]() , ���
, ��� ![]() ��
��
�ڮ�(d��ng)ֱ��l��б�ʲ����ڕr(sh��), ![]() ,
,![]() ,
,
�t![]() ,
,
��� ![]() ,
,![]() ��
��
�ɢ٢ڿɵ�![]() ��
��
�����C��![]() �r(sh��),
�r(sh��), ![]() �����.
�����.
ֱ��lб�ʴ��ڕr(sh��),�O(sh��)ֱ�����̞�![]() .
.
��![]() ��y������:
��y������: ![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]()
![]()
![]()
![]() .
.
�C��,![]() �S�ϴ����c(di��n)
�S�ϴ����c(di��n)![]() ��ʹ��
��ʹ��![]() �����.
�����.


 С�W(xu��)�W(xu��)��(x��)�Î���ϵ�д�
С�W(xu��)�W(xu��)��(x��)�Î���ϵ�д� С�W(xu��)ͬ�����������ܾ�ϵ�д�
С�W(xu��)ͬ�����������ܾ�ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����������w ABCD �У�P��Q�քe���� AB��CD�����c(di��n)��E��F(xi��n)�քe��ֱ��AB��CD�ϵĄ�(d��ng)�c(di��n)��M ��EF �����c(di��n)���t��ʹ�c(di��n) M ��܉�E�LjA�ėl���ǣ� ��
A. PE��QF��2B. PEQF��2
C. PE��2QFD. PE2��QF2��2
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)![]() ���A
���A![]() .
.
��1����ֱ��![]() �^�c(di��n)
�^�c(di��n)![]() �ұ��A
�ұ��A![]() �صõľ����L(zh��ng)��
�صõľ����L(zh��ng)��![]() ����
����![]() �ķ��̣�
�ķ��̣�
��2�����^![]() �c(di��n)�ĈA
�c(di��n)�ĈA![]() ���ҵ����c(di��n)
���ҵ����c(di��n)![]() ��܉�E����.
��܉�E����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����W(xu��)�����n�̣����ڸ����_�O(sh��)�ľ��д�W(xu��)ˮƽ���n�̣�ּ���W(xu��)�������ĸ���������ܴ�W(xu��)˼�S��ʽ���W(xu��)��(x��)������Ӗ(x��n)�������W(xu��)�W(xu��)��(x��)����δ�����I(y��)�������Ü�(zh��n)��.ij���гɹ��_�O(sh��)��W(xu��)�����n�����Ѓ��꣬����250�˅��c�W(xu��)��(x��)�����n�̣��@����W(xu��)��(x��)�����n�̵ČW(xu��)���������˸�У������������ԇ���M��100�֣����Y(ji��)�����±���ʾ��
��?j��n)?sh��) |
|
|
|
|
|
�˔�(sh��) | 25 | 50 | 100 | 50 | 25 |
�������������@��ͨ�^�ĸ��� | 0.9 | 0.8 | 0.6 | 0.4 | 0.3 |
�����@����W(xu��)У�����B(y��ng)����(y��u)����150�ˣ�����(j��)�D�ȸߗl�ΈD�������(y��ng)��(li��n)����������(j��)��(li��n)��z�(y��n)?z��i)ܷ��ڷ��e(cu��)�ĸ��ʲ����^0.01��ǰ�����J(r��n)��W(xu��)��(x��)�����n���c��(y��u)�������P(gu��n)ϵ��
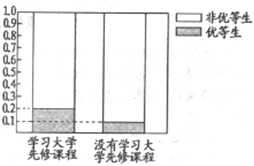
��(y��u)���� | �ǃ�(y��u)���� | ��Ӌ(j��) | |
�W(xu��)��(x��)��W(xu��)�����n�� | 250 | ||
�]�ЌW(xu��)��(x��)��W(xu��)�����n�� | |||
��Ӌ(j��) | 150 |
������֪����ȫУ��150���W(xu��)����(b��o)���W(xu��)��(x��)��W(xu��)�x�(xi��ng)�n�̣����������˸�У������������ԇ����ǰ���ꅢ�Ӵ�W(xu��)�����n�̌W(xu��)��(x��)�ɿ�(j��)���l��������ꅢ�Ӵ�W(xu��)�����n�̌W(xu��)��(x��)�ɿ�(j��)�ĸ���.
�������ڽ��ꅢ�c��W(xu��)�����n�̌W(xu��)��(x��)�ČW(xu��)������ȡһ�ˣ������@�ø�У��������ͨ�^�ĸ��ʣ�
������ij����4���W(xu��)�������˴�W(xu��)�����n�̵ČW(xu��)��(x��)���O(sh��)�@�ø�У��������ͨ�^���˔�(sh��)��![]() ����
����![]() �ķֲ�����ԇ��Ӌ(j��)����ȫУ���Ӵ�W(xu��)�����n�̌W(xu��)��(x��)�ČW(xu��)���@�ø�У��������ͨ�^���˔�(sh��).
�ķֲ�����ԇ��Ӌ(j��)����ȫУ���Ӵ�W(xu��)�����n�̌W(xu��)��(x��)�ČW(xu��)���@�ø�У��������ͨ�^���˔�(sh��).
������(sh��)��(j��)��
| 0.15 | 0.10 | 0��05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
������ʽ��![]() ������
������![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��

��1���C����![]() ƽ��
ƽ��![]() ��
��
��2���ھ���![]() �ϣ��Ƿ����һ�c(di��n)
�ϣ��Ƿ����һ�c(di��n)![]() ��ʹ�ö����
��ʹ�ö����![]() �Ĵ�С��
�Ĵ�С��![]() ��������ڣ���
��������ڣ���![]() ��ֵ����������ڣ�Ո(q��ng)�f�����ɣ�
��ֵ����������ڣ�Ո(q��ng)�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����}�ģ���֪![]() ��ֱ��
��ֱ��![]() �ϵĄ�(d��ng)�c(di��n)���c(di��n)
�ϵĄ�(d��ng)�c(di��n)���c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ���^
���^![]() ��ֱ��
��ֱ��![]() �c
�c![]() ��ֱ������
��ֱ������![]() �c����
�c����![]() �Ĵ�ֱƽ�־��ཻ���c(di��n)
�Ĵ�ֱƽ�־��ཻ���c(di��n)![]() .
.
��1�����c(di��n)![]() ��܉�E
��܉�E![]() �ķ���;
�ķ���;
��2���O(sh��)����![]() �ϵĄ�(d��ng)�c(di��n)
�ϵĄ�(d��ng)�c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q�c(di��n)��
�S��(du��)�Q�c(di��n)��![]() ���c(di��n)
���c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ,ֱ��
,ֱ��![]() �c����
�c����![]() ����һ��(g��)���c(di��n)��
����һ��(g��)���c(di��n)��![]() (
(![]() �c
�c![]() ���غ�)���Ƿ����һ��(g��)���c(di��n)
���غ�)���Ƿ����һ��(g��)���c(di��n)![]() ��ʹ��
��ʹ��![]() ���c(di��n)����?�����ڣ�����c(di��n)
���c(di��n)����?�����ڣ�����c(di��n)![]() ������(bi��o);�������ڣ�Ո(q��ng)�f������.
������(bi��o);�������ڣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����x���^(q��)�g![]() ��
��![]() ��
��![]() ��
��![]() ���L(zh��ng)�Ⱦ���
���L(zh��ng)�Ⱦ���![]() ��������ʽ
��������ʽ![]() �Ľ⼯�ǻ����ཻ�^(q��)�g�IJ������O(sh��)ԓ����ʽ�Ľ⼯�����Ѕ^(q��)�g���L(zh��ng)��֮�͞�
�Ľ⼯�ǻ����ཻ�^(q��)�g�IJ������O(sh��)ԓ����ʽ�Ľ⼯�����Ѕ^(q��)�g���L(zh��ng)��֮�͞�![]() ���t�� ��
���t�� ��
A. ��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() B. ��(d��ng)
B. ��(d��ng)![]() �r(sh��)��
�r(sh��)��![]()
C. ��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() D. ��(d��ng)
D. ��(d��ng)![]() �r(sh��)��
�r(sh��)��![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��![]() .
.
��1����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2���O(sh��)![]() ����
����![]() ��
��![]() �麯��(sh��)
�麯��(sh��)![]() �ăɂ�(g��)��ͬ�Oֵ�c(di��n)���C����
�ăɂ�(g��)��ͬ�Oֵ�c(di��n)���C����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����ˌ�(du��)ij�n�}�M(j��n)���о����÷ӳ�ӷ�����������У![]() ��
��![]() ��
��![]() �����P(gu��n)�ˆT�У���ȡ�����˽M���о�С�M�����P(gu��n)��(sh��)��(j��)Ҋ�±�����λ���ˣ�.
�����P(gu��n)�ˆT�У���ȡ�����˽M���о�С�M�����P(gu��n)��(sh��)��(j��)Ҋ�±�����λ���ˣ�.
��У | ���P(gu��n)�ˆT | ��ȡ�˔�(sh��) |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
��1����![]() ��
��![]() ��
��
��2����ĸ�У![]() ��
��![]() ��ȡ�������x2�������}�l(f��)�ԣ����@2�˶����Ը�У
��ȡ�������x2�������}�l(f��)�ԣ����@2�˶����Ը�У![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com