，向量
。
的特征值和特征向量；
.
時的一個特征向量為
，特征值
時的一個特征向量為
，（2）
=0得特征值
，當(dāng)時，代入二元一次方程組
解得
；∴特征值時的一個特征向量為，當(dāng)時，代入二元一次方程組解得
∴特征值時的一個特征向量為 ，（2）本題可直接求出
，再根據(jù)矩陣運(yùn)算法則求出.也可利用特征值和特征向量的性質(zhì)進(jìn)行化簡. 4分
解得A的特征值 6分時，代入二元一次方程組解得時的一個特征向量為 8分時，代入二元一次方程組解得時的一個特征向量為 10分，
則
12分
14分
16分
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源：不詳 題型：解答題
| ||
| z+i |
查看答案和解析>>
科目：高中數(shù)學(xué) 來源：不詳 題型：填空題
查看答案和解析>>
科目：高中數(shù)學(xué) 來源：不詳 題型：填空題
（
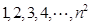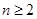）任意排成
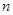行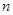列的數(shù)表.對于某一個數(shù)表，計(jì)算各行和各列中的任意兩個數(shù)
（
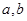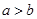）的比值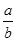
，稱這些比值中的最小值為這個數(shù)表的“特征值”.若
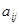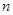表示某個行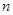列數(shù)表中第
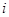行第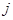
列的數(shù)（
，
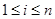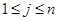），且滿足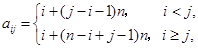
，當(dāng)
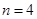時數(shù)表的“特征值”為_________查看答案和解析>>
科目：高中數(shù)學(xué) 來源：不詳 題型：解答題
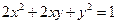在矩陣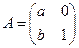
（其中a＞0）對應(yīng)的變換作用下得到的曲線為
．
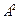的逆矩陣．查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
（
，
為實(shí)數(shù)）．若矩陣
屬于特征值2，3的一個特征向量分別為
，
，求矩陣
的逆矩陣
．
，N＝
，求二階方陣X，使MX＝N.
，向量α＝
，β＝
.
β在TM作用下的象；
=
M
成立的矩陣M.