
【題目】設函數(shù)![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)當![]() 時,
時, ![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析(2)![]() .
.
【解析】試題分析:(1)根據(jù)![]() ,對字母a分類討論,求出函數(shù)的單調區(qū)間;(2)當
,對字母a分類討論,求出函數(shù)的單調區(qū)間;(2)當![]() 時,分離參數(shù),轉化為分別求
時,分離參數(shù),轉化為分別求![]() 的最小值,及
的最小值,及![]() 的最大值,利用導數(shù),求其
的最大值,利用導數(shù),求其![]() 最大值即可.
最大值即可.
試題解析:(1)![]() .
.
若![]() ,則
,則![]() ,在
,在![]() 單調遞增.若
單調遞增.若![]() ,當
,當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .于是
.于是![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
(2)方法1:當![]() 時,
時, ![]() ,即
,即![]()
因為函數(shù)![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]() .
.
設![]() ,
, ![]() ,當
,當![]() 時,
時, ![]() ,
, ![]() 單調遞增;當
單調遞增;當![]() 時,
時, ![]() ,
, ![]() 單調遞減.故
單調遞減.故![]()
![]() ,所以
,所以![]() .綜上,
.綜上, ![]() 的取值范圍為
的取值范圍為![]() .
.
(2)方法2:設![]() ,則當
,則當![]() 時,
時, ![]() .
.
由![]() ,得
,得![]() .
.
![]() ,當
,當![]() 時,
時, ![]() ,
, ![]() 單調遞增,所以
單調遞增,所以![]() .
.
若![]() ,當
,當![]() 時,
時, ![]() ,
, ![]() 單調遞增,故
單調遞增,故![]() .因為
.因為![]() ,所以
,所以![]() .
.
若![]() ,由
,由![]() ,
, ![]() ,知
,知![]() 在
在![]() 存在唯一零點,設為
存在唯一零點,設為![]() ,則
,則![]() .
.
當![]() 時,
時, ![]() ,
, ![]() 單調遞減;當
單調遞減;當![]() 時,
時, ![]() ,
, ![]() 單調遞增;故
單調遞增;故![]() 在
在![]() 有最小值
有最小值![]() ,而
,而![]() .由
.由![]() 得
得![]() .
.
由(1)得![]() 在
在![]() 單調遞減,所以
單調遞減,所以![]() .
.
綜上, ![]() 的取值范圍為
的取值范圍為![]() .
.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】設數(shù)列{an}的前n項和為Sn,且Sn=4an﹣p,其中p是不為零的常數(shù).
(1)證明:數(shù)列{an}是等比數(shù)列;
(2)當p=3時,若數(shù)列{bn}滿足bn+1=bn+an(n∈N*),b1=2,求數(shù)列{bn}的通項公式.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,已知兩個正方形ABCD和DCEF不在同一平面內,M,N分別為AB,DF的中點.
(1)若平面ABCD⊥平面DCEF,求直線MN與平面DCEF所成角的正弦值;
(2)用反證法證明:直線ME與BN是兩條異面直線.
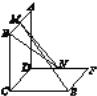
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)的導函數(shù)f′(x),且對任意x>0,都有f′(x)>![]() .
.
(1)判斷函數(shù)F(x)=![]() 在(0,+∞)上的單調性;
在(0,+∞)上的單調性;
(2)設x1,x2∈(0,+∞),證明:f(x1)+f(x2)<f(x1+x2);
(3)請將(2)中結論推廣到一般形式,并證明你所推廣的結論.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(![]() )求
)求![]() 的單調區(qū)間.
的單調區(qū)間.
(![]() )證明:當
)證明:當![]() 時,方程
時,方程![]() 在區(qū)間
在區(qū)間![]() 上只有一個零點.
上只有一個零點.
(![]() )設
)設![]() ,其中
,其中![]() 若
若![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市高中全體學生參加某項測評,按得分評為![]() 兩類(評定標準見表1).根據(jù)男女學生比例,使用分層抽樣的方法隨機抽取了10000名學生的得分數(shù)據(jù),其中等級為
兩類(評定標準見表1).根據(jù)男女學生比例,使用分層抽樣的方法隨機抽取了10000名學生的得分數(shù)據(jù),其中等級為![]() 的學生中有40%是男生,等級為
的學生中有40%是男生,等級為![]() 的學生中有一半是女生.等級為
的學生中有一半是女生.等級為![]() 和
和![]() 的學生統(tǒng)稱為
的學生統(tǒng)稱為![]() 類學生,等級為
類學生,等級為![]() 和
和![]() 的學生統(tǒng)稱為
的學生統(tǒng)稱為![]() 類學生.整理這10000名學生的得分數(shù)據(jù),得到如圖2所示的頻率分布直方圖,
類學生.整理這10000名學生的得分數(shù)據(jù),得到如圖2所示的頻率分布直方圖,
類別 | 得分( | |
|
|
|
|
| |
|
|
|
|
| |
表1
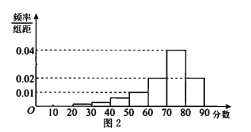
(I)已知該市高中學生共20萬人,試估計在該項測評中被評為![]() 類學生的人數(shù);
類學生的人數(shù);
(Ⅱ)某5人得分分別為45,50,55,75,85.從這5人中隨機選取2人組成甲組,另外3人組成乙組,求“甲、乙兩組各有1名![]() 類學生”的概率;
類學生”的概率;
(Ⅲ)在這10000名學生中,男生占總數(shù)的比例為51%, ![]() 類女生占女生總數(shù)的比例為
類女生占女生總數(shù)的比例為![]() ,
, ![]() 類男生占男生總數(shù)的比例為
類男生占男生總數(shù)的比例為![]() ,判斷
,判斷![]() 與
與![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com