
【題目】已知數(shù)列![]() 是公差為正數(shù)的等差數(shù)列,其前
是公差為正數(shù)的等差數(shù)列,其前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]() ,
, ![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)數(shù)列![]() 滿(mǎn)足
滿(mǎn)足![]() ,
, ![]() .①求數(shù)列
.①求數(shù)列![]() 的通項(xiàng)公式;②是否存在正整數(shù)
的通項(xiàng)公式;②是否存在正整數(shù)![]() ,
, ![]() (
(![]() ),使得
),使得![]() ,
, ![]() ,
, ![]() 成等差數(shù)列?若存在,求出
成等差數(shù)列?若存在,求出![]() ,
, ![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
【答案】(1) ![]() ;(2) ①
;(2) ①![]() ;②存在正整數(shù)
;②存在正整數(shù)![]() ,
, ![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() 成等差數(shù)列.
成等差數(shù)列.
【解析】試題分析:(1)直接由已知列關(guān)于首項(xiàng)和公差的方程組,求解方程組得首項(xiàng)和公差,代入等差數(shù)列的通項(xiàng)公式得答案;(2)①把數(shù)列![]() 的通項(xiàng)公式代入
的通項(xiàng)公式代入![]() ,然后裂項(xiàng),累加后即可求得數(shù)列
,然后裂項(xiàng),累加后即可求得數(shù)列![]() 的通項(xiàng)公式;②假設(shè)存在正整數(shù)
的通項(xiàng)公式;②假設(shè)存在正整數(shù)![]() ,
, ![]() (
(![]() ),使得
),使得![]() ,
, ![]() ,
, ![]() 成等差數(shù)列,則
成等差數(shù)列,則![]() ,由此列關(guān)于
,由此列關(guān)于![]() 的方程,求解得答案.
的方程,求解得答案.
試題解析:(1)設(shè)數(shù)列![]() 的公差為
的公差為![]() ,則
,則![]() .
.
由![]() ,
, ![]() ,得
,得![]() 解得
解得![]() 或
或![]() (舍去).
(舍去).
所以![]() .
.
(2)①因?yàn)?/span>![]() ,
, ![]() ,所以
,所以![]() ,
,
![]() ,
,
即![]() ,
, ![]() ,…,
,…, ![]() ,(
,( ![]() )
)
累加得![]() ,所以
,所以![]() ,
,
![]() 也符合上式,故
也符合上式,故![]() ,
, ![]() .
.
②假設(shè)存在正整數(shù)![]() 、
、![]() (
(![]() ),使得
),使得![]() ,
, ![]() ,
, ![]() 成等差數(shù)列,則
成等差數(shù)列,則![]() .
.
又![]() ,
, ![]() ,
, ![]() ,
,
所以![]()
![]() ,即
,即![]() ,
,
化簡(jiǎn)得: ![]()
![]() ,
,
當(dāng)![]() ,即
,即![]() 時(shí),
時(shí), ![]() (舍去);
(舍去);
當(dāng)![]() ,即
,即![]() 時(shí),
時(shí), ![]() 符合題意.
符合題意.
所以存在正整數(shù)![]() ,
, ![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() 成等差數(shù)列.
成等差數(shù)列.


 期末100分闖關(guān)海淀考王系列答案
期末100分闖關(guān)海淀考王系列答案 小學(xué)能力測(cè)試卷系列答案
小學(xué)能力測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,圓![]() :
: ![]() .
.
(1)若圓![]() 與
與![]() 軸相切,求圓
軸相切,求圓![]() 的方程;
的方程;
(2)求圓心![]() 的軌跡方程;
的軌跡方程;
(3)已知![]() ,圓
,圓![]() 與
與![]() 軸相交于兩點(diǎn)
軸相交于兩點(diǎn)![]() (點(diǎn)
(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè)).過(guò)點(diǎn)
的左側(cè)).過(guò)點(diǎn)![]() 任作一條直線與圓
任作一條直線與圓![]() :
: ![]() 相交于兩點(diǎn)
相交于兩點(diǎn)![]() .問(wèn):是否存在實(shí)數(shù)
.問(wèn):是否存在實(shí)數(shù)![]() ,使得
,使得![]() ?若存在,求出實(shí)數(shù)
?若存在,求出實(shí)數(shù)![]() 的值,若不存在,請(qǐng)說(shuō)明理由.
的值,若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)= ![]() 為奇函數(shù).
為奇函數(shù).
(1)求實(shí)數(shù)m的值;
(2)用定義證明函數(shù)f(x)在區(qū)間(0,+∞)上為單調(diào)減函數(shù);
(3)若關(guān)于x的不等式f(x)+a<0對(duì)區(qū)間[1,3]上的任意實(shí)數(shù)x都成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓x2+y2=4上一定點(diǎn)A(2,0),B(1,1)為圓內(nèi)一點(diǎn),P,Q為圓上的動(dòng)點(diǎn). 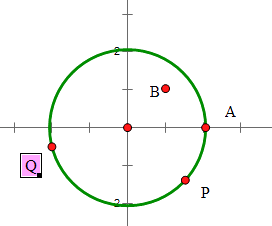
(1)求線段AP中點(diǎn)的軌跡方程;
(2)若∠PBQ=90°,求線段PQ中點(diǎn)的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某研究所計(jì)劃利用宇宙飛船進(jìn)行新產(chǎn)品搭載試驗(yàn),計(jì)劃搭載若干件新產(chǎn)品A,B,該研究所要根據(jù)產(chǎn)品的研制成本、產(chǎn)品重量、搭載試驗(yàn)費(fèi)用和預(yù)計(jì)收益來(lái)決定具體安排,通過(guò)調(diào)查得到的有關(guān)數(shù)據(jù)如表:
每件A產(chǎn)品 | 每件B產(chǎn)品 | |
研制成本、搭載試驗(yàn)費(fèi)用之和(萬(wàn)元) | 20 | 30 |
產(chǎn)品重量(千克) | 10 | 5 |
預(yù)計(jì)收益(萬(wàn)元) | 80 | 60 |
已知研制成本、搭載試驗(yàn)費(fèi)用之和的最大資金為300萬(wàn)元,最大搭載重量為110千克,則如何安排這兩種產(chǎn)品進(jìn)行搭載,才能使總預(yù)計(jì)收益達(dá)到最大,求最大預(yù)計(jì)收益是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列{an} 的前n項(xiàng)和Sn=3n2+8n,{bn}是等差數(shù)列,且an=bn+bn+1
(1)求數(shù)列{bn}的通項(xiàng)公式;
(2)令cn= ![]() ,求數(shù)列{cn}的前n項(xiàng)和Tn .
,求數(shù)列{cn}的前n項(xiàng)和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某個(gè)年級(jí)有男生560人,女生420人,用分層抽樣的方法從該年級(jí)全體學(xué)生中抽取一個(gè)容量為280的樣本,則此樣本中男生人數(shù)為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知向量 ![]() 與向量
與向量 ![]() =(2,﹣1,2)共線,且滿(mǎn)足
=(2,﹣1,2)共線,且滿(mǎn)足 ![]()
![]() =18,(k
=18,(k ![]() +
+ ![]() )⊥(k
)⊥(k ![]() ﹣
﹣ ![]() ),求向量
),求向量 ![]() 及k的值.
及k的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com