已知數(shù)列{
bn}是等差數(shù)列,
b1=1,
b1+
b2+…+
b10=145.
(1)求數(shù)列{
bn}的通項公式
bn;
(2)設(shè)數(shù)列{
an}的通項
an=log
a(1+
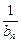
)(其中
a>0且
a≠1)記
Sn是數(shù)列{
an}的前
n項和,試比較
Sn與
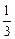
log
abn+1的大小,并證明你的結(jié)論
(1)
bn=3
n-2(2)當
a>1時,
Sn>

log
abn+1?,當 0<
a<1時,
Sn<

log
abn+1設(shè)數(shù)列{
bn}的公差為
d,由題意得
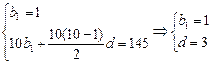
,∴
bn=3
n-2
(2)證明:由
bn=3
n-2知
Sn=log
a(1+1)+log
a(1+
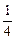
)+…+log
a(1+
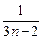
)
=log
a[(1+1)(1+
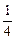
)…(1+
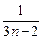
)]
而

log
abn+1=log
a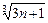
,于是,比較
Sn與

log
abn+1?的大小
比較(1+1)(1+
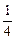
)…
(1+
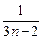
)與
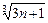
的大小.
取
n=1,有(1+1)=
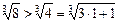
取
n=2,有(1+1)(1+
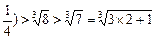
推測:(1+1)(1+
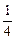
)…(1+
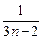
)>
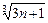
(
*)
①當
n=1時,已驗證(
*)式成立.
②假設(shè)
n=
k(
k≥1)時(
*)式成立,即(1+1)(1+
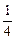
)…(1+
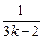
)>
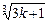
則當
n=
k+1時,
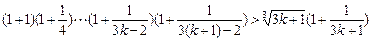
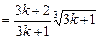
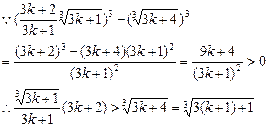
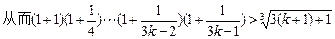
,即當
n=
k+1時,(
*)式成立
由①②知,(
*)式對任意正整數(shù)
n都成立.
于是,當
a>1時,
Sn>

log
abn+1?,當 0<
a<1時,
Sn<

log
abn+1
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)用數(shù)學(xué)歸納法證明:
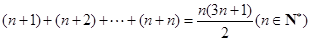
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知x,y∈Z,n∈N
*,設(shè)f(n)是不等式組
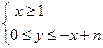
表示的平面區(qū)域內(nèi)可行解的個數(shù),則f(1)=
_______;f(2)=
_______;f(n)=
_______.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
由下列各式:
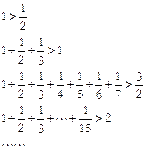
你能得出怎樣的結(jié)論,并進行證明.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
用數(shù)學(xué)歸納法證明
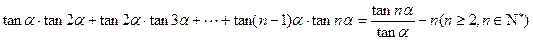
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知

.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
用數(shù)學(xué)歸納法證明:
當
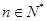
時,

成立
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
用數(shù)學(xué)歸納法證

的過程中,當n=k到n=k+1時,左邊所增加的項為________________
查看答案和解析>>

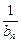 )(其中a>0且a≠1)記Sn是數(shù)列{an}的前n項和,試比較Sn與
)(其中a>0且a≠1)記Sn是數(shù)列{an}的前n項和,試比較Sn與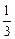 logabn+1的大小,并證明你的結(jié)論
logabn+1的大小,并證明你的結(jié)論 logabn+1?,當 0<a<1時,Sn<
logabn+1?,當 0<a<1時,Sn< logabn+1
logabn+1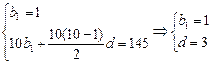 ,∴bn=3n-2
,∴bn=3n-2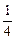 )+…+loga(1+
)+…+loga(1+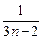 )
)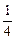 )…(1+
)…(1+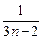 )]
)] logabn+1=loga
logabn+1=loga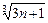 ,于是,比較Sn與
,于是,比較Sn與 logabn+1?的大小
logabn+1?的大小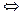 比較(1+1)(1+
比較(1+1)(1+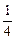 )…
)…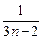 )與
)與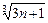 的大小.
的大小.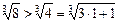
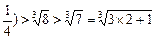
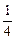 )…(1+
)…(1+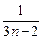 )>
)>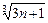 (*)
(*)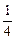 )…(1+
)…(1+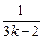 )>
)>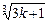
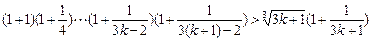
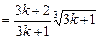
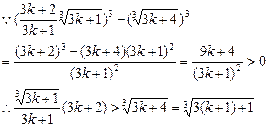
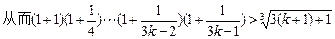 ,即當n=k+1時,(*)式成立
,即當n=k+1時,(*)式成立 logabn+1?,當 0<a<1時,Sn<
logabn+1?,當 0<a<1時,Sn< logabn+1
logabn+1

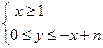 表示的平面區(qū)域內(nèi)可行解的個數(shù),則f(1)=_______;f(2)=_______;f(n)=_______.
表示的平面區(qū)域內(nèi)可行解的個數(shù),則f(1)=_______;f(2)=_______;f(n)=_______.