【題目】在四棱錐P﹣ABCD中，各側面是全等的等腰三角形，腰長為4且頂角為30°，底面是正方形（如圖），在棱PB，PC上各有一點M，N，且四邊形AMND的周長最小，點S從A出發依次沿四邊形AM，MN，ND運動至點D，記點S行進的路程為x，棱錐S﹣ABCD的體積為V（x），則函數V（x）的圖象是（ ）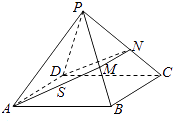 
A.
B.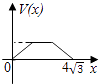
C.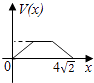
D.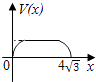
科目：高中數學 來源： 題型：
【題目】某市在對高三學生的4月理科數學調研測試的數據統計顯示，全市10000名學生的成績服從正態分布
，現從甲校100分以上（含100分）的200份試卷中用系統抽樣的方法抽取了20份試卷來分析，統計如下：
（注：表中試卷編號
）
（1）列出表中試卷得分為126分的試卷編號（寫出具體數據）；
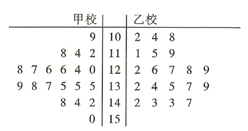
（2）該市又從乙校中也用系統抽樣的方法抽取了20份試卷，將甲乙兩校這40份試卷的得分制作了莖葉圖（如圖6），試通過莖葉圖比較兩校學生成績的平均分及分散程度（均不要求計算出具體值，給出結論即可）；
（3）在第（2）問的前提下，從甲乙兩校這40名學生中，從成績在140分以上（含140分）的學生中任意抽取3人，該3人在全市前15名的人數記為
，求
的分布列和期望.
（附：若隨機變量
服從正態分布
，則
， 
， 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的前n項和為Sn ， 且a1+a3=10，S4=24．
（1）求數列{an}的通項公式；
（2）令Tn= 
，求證：Tn＜ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在銳角△ABC中，a、b、c分別為∠A、∠B、∠C所對的邊，且 
a=2csinA．
（1）確定∠C的大小；
（2）若c= ，求△ABC周長的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列向量組中，能作為表示它們所在平面內所有向量的一組基底的是（ ）
A.
=（0，0） 
=（1，﹣2）
B.
=（﹣1，2） =（3，7）
C.=（3，5） =（6，10）
D.=（2，﹣3） =（ 
，﹣ 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（ex ， lnx+k）， 
=（1，f（x））， ∥ （k為常數，e是自然對數的底數），曲線y=f（x）在點（1，f（1））處的切線與y軸垂直，F（x）=xexf′（x）．
（1）求k的值及F（x）的單調區間；
（2）已知函數g（x）=﹣x2+2ax（a為正實數），若對任意x2∈[0，1]，總存在x1∈（0，+∞），使得g（x2）＜F（x1），求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
