【題目】已知函數
.
（1）求函數
的極值點；
（2）設
，若函數
在
內有兩個極值點
，求證： 
.
【答案】(1)詳見解析;(2)詳見解析.
【解析】試題分析：（1）求出
的導數，并分解因式，對
討論，分
， 
求得
的范圍，可得函數
增區間， 
求得
的范圍，可得函數
的減區間，可得所求極值點；（2）求出
的解析式和導數，由題意可得
有兩個不為
的正根，運用判別式大于零和韋達定理，可得
，化簡
，由不等式的性質即可得證.
試題解析：（1）∵
①若
，由
得
；由
，可得
，即函數
在
上為增函數；由
，可得
，即函數
在
上為減函數，所以函數
在
上有唯一的極小值點
，無極大值點.
②若
，由
得
；由
，可得
或
，即函數
在
上為增函數；由
，可得
，即函數
在
上為減函數，所以函數
在
上有極大值點
，極小值點
.
③若
，則
，在
上大于等于零恒成立，故函數
在
上單調遞增，無極值點.
④ 若
，由
得
；由
可得
或
，所以函數
在
上為增函數；由
，可得
，所以函數
在
上為減函數，所以函數
在
上有極大值點
，極小值點
.
（2）
，則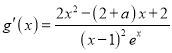
記
，由題意可知方程
即
在
上有兩個不等實數根
.所以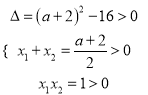
解得： 
∵
∴
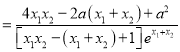
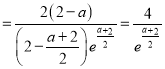
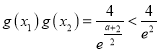
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax2+ln（x+1）．
（1）當a=﹣ 
時，求函數f（x）的單調區間；
（2）若函數f（x）在區間[1，+∞）上為減函數，求實數a的取值范圍；
（3）當x∈[0，+∞）時，不等式f（x）﹣x≤0恒成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著資本市場的強勢進入，互聯網共享單車“忽如一夜春風來”，遍布了一二線城市的大街小巷.為了解共享單車在
市的使用情況，某調查機構借助網絡進行了問卷調查，并從參與調查的網友中抽取了200人進行抽樣分析，得到表格：（單位：人）
經常使用 | 偶爾或不用 | 合計 | |
30歲及以下 | 70 | 30 | 100 |
30歲以上 | 60 | 40 | 100 |
合計 | 130 | 70 | 200 |
（1）根據以上數據，能否在犯錯誤的概率不超過0.15的前提下認為
市使用共享單車情況與年齡有關？
（2）現從所抽取的30歲以上的網友中利用分層抽樣的方法再抽取5人.
（i）分別求這5人中經常使用、偶爾或不用共享單車的人數；
（ii）從這5人中，再隨機選出2人贈送一件禮品，求選出的2人中至少有1人經常使用共享單車的概率.
參考公式： 
，其中
.
參考數據：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
x3﹣x2﹣ 
x，則f（﹣a2）與f（﹣1）的大小關系為（ ）
A.f（﹣a2）≤f（﹣1）
B.f（﹣a2）＜f（﹣1）
C.f（﹣a2）≥f（﹣1）
D.f（﹣a2）與f（﹣1）的大小關系不確定
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個口袋內有4個不同的紅球，6個不同的白球，
（1）從中任取4個球，紅球的個數不比白球少的取法有多少種？
（2）若取一個紅球記2分，取一個白球記1分，從中任取5個球，使總分不少于7分的取法有多少種？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正四棱柱ABCD﹣A1B1C1D1中，AA1=2AB．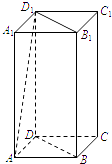
（1）求AD1與面BB1D1D所成角的正弦值；
（2）點E在側棱AA1上，若二面角E﹣BD﹣C1的余弦值為 
，求 
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現有一個關于平面圖形的命題：如圖，同一個平面內有兩個邊長都是a的正方形，其中一個的某頂點在另一個的中心，則這兩個正方形重疊部分的面積恒為 
．類比到空間，有兩個棱長均為a的正方體，其中一個的某頂點在另一個的中心，則這兩個正方體重疊部分的體積恒為 ．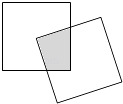 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
