
���}Ŀ����֪����(sh��)![]() ������
������![]() ����Ȼ��(du��)��(sh��)�ĵה�(sh��)��
����Ȼ��(du��)��(sh��)�ĵה�(sh��)��
����ԇ�Дຯ��(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
����(d��ng)![]() �r(sh��)������ʽ
�r(sh��)������ʽ![]() ���������(sh��)��(sh��)
���������(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
���𰸡�(��)Ҋ������ (��) ![]()
��������
�������ԭ����(sh��)�Č�(d��o)����(sh��)��Ȼ��(du��)a�����(d��ng)a��0�r(sh��)��![]() ��0��f��x����R�ϵĜp����(sh��)����(d��ng)a��0�r(sh��)���Ɍ�(d��o)����(sh��)��0��Ì�(d��o)����(sh��)�����c(di��n)�����Ɍ�(d��o)����(sh��)�����c(di��n)��(du��)���x��ֶΣ�����(j��)��(d��o)����(sh��)�ڸ���(n��i)�ķ�̖(h��o)�õ�ԭ����(sh��)�Ć��{(di��o)�ԣ�
��0��f��x����R�ϵĜp����(sh��)����(d��ng)a��0�r(sh��)���Ɍ�(d��o)����(sh��)��0��Ì�(d��o)����(sh��)�����c(di��n)�����Ɍ�(d��o)����(sh��)�����c(di��n)��(du��)���x��ֶΣ�����(j��)��(d��o)����(sh��)�ڸ���(n��i)�ķ�̖(h��o)�õ�ԭ����(sh��)�Ć��{(di��o)�ԣ�
�����x����(sh��)t���ɵ�![]() ���������
���������![]() ���t���}�ȃr(ji��)����⺯��(sh��)g��x������Сֵ��Ȼ�����Ì�(d��o)��(sh��)������⺯��(sh��)g��x������Сֵ�ô𰸣�
���t���}�ȃr(ji��)����⺯��(sh��)g��x������Сֵ��Ȼ�����Ì�(d��o)��(sh��)������⺯��(sh��)g��x������Сֵ�ô𰸣�
�������}�ɵú���(sh��)![]() �Ķ��x��?y��n)?/span>
�Ķ��x��?y��n)?/span>![]() ��
��![]() ��
��
��(d��ng)![]() �r(sh��)����?y��n)?/span>
�r(sh��)����?y��n)?/span>![]() ������
������![]() �����Ժ���(sh��)
�����Ժ���(sh��)![]() ��
��![]() �φ��{(di��o)�f�p��
�φ��{(di��o)�f�p��
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() �����
�����![]() ����
����![]() �����
�����![]() ��
��
���Ժ���(sh��)![]() ��
��![]() �φ��{(di��o)�f�p����
�φ��{(di��o)�f�p����![]() �φ��{(di��o)�f����
�φ��{(di��o)�f����
�C�ϣ���(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() ��
��![]() �φ��{(di��o)�f�p����(d��ng)
�φ��{(di��o)�f�p����(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() ��
��![]() �φ��{(di��o)�f�p����
�φ��{(di��o)�f�p����![]() �φ��{(di��o)�f����
�φ��{(di��o)�f����
����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��
�t����ʽ![]() �ɻ���
�ɻ���![]() ��
��
��?y��n)鲻���?/span>![]() �����������ԭ���}���D(zhu��n)����
�����������ԭ���}���D(zhu��n)����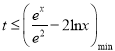 ��
��
�O(sh��)![]() ���@Ȼ����(sh��)
���@Ȼ����(sh��)![]() �Ķ��x��?y��n)?/span>
�Ķ��x��?y��n)?/span>![]() ��
��![]() ��
��
��![]() ���t
���t![]() �������
�������
���Ժ���(sh��)![]() ��
��![]() �φ��{(di��o)�f����
�φ��{(di��o)�f����
��![]() �����Ԯ�(d��ng)
�����Ԯ�(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ����(d��ng)
����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��
���Ժ���(sh��)![]() ��
��![]() �φ��{(di��o)�f�p����
�φ��{(di��o)�f�p����![]() �φ��{(di��o)�f����
�φ��{(di��o)�f����
����![]() ������
������![]() ��
��
�ʌ�(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)![]() ���A
���A![]() ���c(di��n)
���c(di��n)![]() �LjA��һ��(d��ng)�c(di��n)��
�LjA��һ��(d��ng)�c(di��n)�� ![]() �Ĵ�ֱƽ�־��c
�Ĵ�ֱƽ�־��c![]() �����c(di��n)
�����c(di��n)![]() .
.
��1�����c(di��n)![]() ��܉�E���̣�
��܉�E���̣�
��2���O(sh��)�c(di��n)![]() ��܉�E������
��܉�E������![]() ���^�c(di��n)
���^�c(di��n)![]() ��б�ʲ���0��ֱ��
��б�ʲ���0��ֱ��![]() �c
�c![]() ����
����![]() ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)![]() �P(gu��n)��
�P(gu��n)��![]() �S��(du��)�Q�c(di��n)��
�S�Č�(du��)�Q�c(di��n)��![]() ���C��ֱ��
���C��ֱ��![]() �^���c(di��n)������
�^���c(di��n)������![]() ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪A,B���c(di��n)������PC��ֱ������O�ı����ϣ�AB��BC��AB=2��BC=4������O���w�e��![]() ���t�����FP-ABC����e��___________��
���t�����FP-ABC����e��___________��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij�t(y��)ˎ��˾�аl(f��)һ�N�µı����a(ch��n)Ʒ�������a(ch��n)��һ���a(ch��n)Ʒ�г�ȡ200������ӱ����y(c��)���a(ch��n)Ʒ��һ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ��ԓָ��(bi��o)ֵԽ��Խ��.�ɜy(c��)���Y(ji��)���õ������l�ʷֲ�ֱ���D��
������![]() ����ԇ��Ӌ(j��)�@200�Юa(ch��n)Ʒ��ԓ�(xi��ng)ָ��(bi��o)��ƽ��ֵ��
����ԇ��Ӌ(j��)�@200�Юa(ch��n)Ʒ��ԓ�(xi��ng)ָ��(bi��o)��ƽ��ֵ��
����(gu��)�����P(gu��n)���TҎ(gu��)��ÿ�Юa(ch��n)Ʒԓ�(xi��ng)ָ��(bi��o)ֵ������150����ϸ��Ұ�ָ��(bi��o)ֵ�ďĵ͵������η֞飺�ϸ�(y��u)������(y��u)������(g��)�ȼ�(j��)������![]() �郞(y��u)����������185��ϸ�����215�郞(y��u)��.�Øӱ���ԓ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ���l�ʴ���a(ch��n)Ʒ��ԓ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ�ĸ���.
�郞(y��u)����������185��ϸ�����215�郞(y��u)��.�Øӱ���ԓ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ���l�ʴ���a(ch��n)Ʒ��ԓ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ�ĸ���.
����a(ch��n)Ʒԓ�(xi��ng)ָ��(bi��o)ֵ�ă�(y��u)���ʣ�
�ڬF(xi��n)���@���a(ch��n)Ʒ���S�C(j��)��ȡ3�У�������������1��ԓ�(xi��ng)�|(zh��)��ָ��(bi��o)ֵ�郞(y��u)��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У���֪?ji��ng)�ֱ��
�У���֪?ji��ng)�ֱ��![]() �ą���(sh��)���̣�
�ą���(sh��)���̣�![]() ����
����![]() �酢��(sh��)��
�酢��(sh��)��![]() �� ��������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�� ��������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�������S��O�S�����O����(bi��o)ϵ������
�S�������S��O�S�����O����(bi��o)ϵ������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() .
.
����������![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
������ֱ��![]() �c����
�c����![]() ǡ����2��(g��)�����c(di��n)�r(sh��)����ֱ��
ǡ����2��(g��)�����c(di��n)�r(sh��)����ֱ��![]() ��һ�㷽��.
��һ�㷽��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
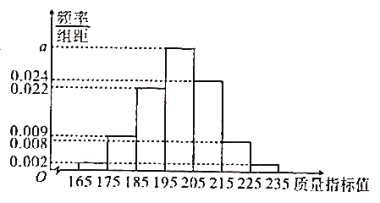
���}Ŀ����ӭ��2022�걱�������W�\(y��n)��(hu��)���ռ����W֪�R(sh��)��ijУ�_չ������ѩ���}�������W֪�R(sh��)��(j��ng)ِ���(d��ng)���F(xi��n)�ą��Ӷ��W֪�R(sh��)��(j��ng)ِ���(d��ng)�ČW(xu��)�����S�C(j��)��ȡ��100���W(xu��)�����������ı�ِ�ɿ�(j��)���M�֞�100�֣��֞�6�M��![]() ��
��![]() �õ���D��ʾ���l�ʷֲ�ֱ���D��
�õ���D��ʾ���l�ʷֲ�ֱ���D��
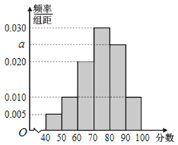
������![]() ��ֵ��
��ֵ��
����ӛ![]() ��ʾ�¼����ą��Ӷ��W֪�R(sh��)��(j��ng)ِ���(d��ng)�ČW(xu��)�����S�C(j��)��ȡһ���W(xu��)����ԓ�W(xu��)���ı�ِ�ɿ�(j��)������80��������Ӌ(j��)
��ʾ�¼����ą��Ӷ��W֪�R(sh��)��(j��ng)ِ���(d��ng)�ČW(xu��)�����S�C(j��)��ȡһ���W(xu��)����ԓ�W(xu��)���ı�ِ�ɿ�(j��)������80��������Ӌ(j��)![]() �ĸ��ʣ�
�ĸ��ʣ�
�����ڳ�ȡ��100���W(xu��)���У�Ҏ(gu��)������ِ�ɿ�(j��)������80�֞�����(y��u)��������ِ�ɿ�(j��)����80�֞����ǃ�(y��u)������Ո(q��ng)?ji��n)ڴ��}���ό�![]() ��(li��n)���a(b��)�����������Д��Ƿ���
��(li��n)���a(b��)�����������Д��Ƿ���![]() �İ����J(r��n)������ِ�ɿ�(j��)�Ƿ�(y��u)���c�Ԅe���P(gu��n)����
�İ����J(r��n)������ِ�ɿ�(j��)�Ƿ�(y��u)���c�Ԅe���P(gu��n)����
������ʽ����(sh��)��(j��)��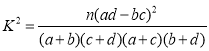 ��
��![]() ��
��
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���Ї�(gu��)�ĸ��_���ԁ�(l��i)��(j��ng)��(j��)�l(f��)չѸ�ͣ�ijһ�����еij��(zh��n)����2012��2018���˾���֧��������ɢ�c(di��n)�D���£���ݾ���ĩλ��(sh��)�֜p1��ʾ��.
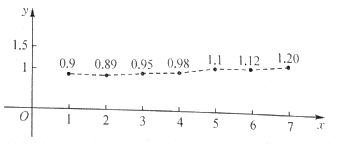
��1����ɢ�c(di��n)�D��֪���˾���֧��������y���f(w��n)Ԫ���c���x֮�g�����^��(qi��ng)�ľ������P(gu��n)�P(gu��n)ϵ��ԇ��y�P(gu��n)��x�Ļؚw���̣�ϵ��(sh��)���_��0.001�����������P(gu��n)�P(gu��n)ϵ�A(y��)�y(c��)2019��ԓ�����˾���֧�������룻
��2����2014��2018����傀(g��)������S�C(j��)��ȡ�ɂ�(g��)��(sh��)��(j��)���ӱ�����������ȡ�ăɂ�(g��)��(sh��)��(j��)�У��˾���֧��������ǡ����һ��(g��)���^1�f(w��n)Ԫ�ĸ���.
ע�� ��
��![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��2020��������ʼ�����ڠ����(l��i)��(sh��)����������ʹ�ø��،W(xu��)���ں��ٽY(ji��)��֮��o(w��)����У���������ʹ�����˾��Ͻ̌W(xu��)���h(yu��n)�̽̌W(xu��)��ͣ�n��ͣ�W(xu��)��Ҫ��Ҳ�õ��˼��L(zh��ng)����ٝͬ�����،W(xu��)У�_չ��ʽ���ӵľ��Ͻ̌W(xu��)��ij�،W(xu��)У���˼ӏ�(qi��ng)�W(xu��)���ۇ�(gu��)�������M�_�O(sh��)��(gu��)�W(xu��)�n�������˽�W(xu��)��ϲ�g��(gu��)�W(xu��)�Ƿ��c�Ԅe���P(gu��n)��ԓ�W(xu��)У��(du��)100���W(xu��)���M(j��n)���ˆ����{(di��o)�飬�õ�������(li��n)����
ϲ�g��(gu��)�W(xu��) | ��ϲ�g��(gu��)�W(xu��) | ��Ӌ(j��) | |
���� | 20 | 50 | |
�� | 10 | ||
��Ӌ(j��) | 100 |
��1��Ո(q��ng)��������(li��n)���a(b��)�����������Д��ܷ��ڷ��e(cu��)�`�ĸ��ʲ����^0.001��ǰ�����J(r��n)��ϲ�g��(gu��)�W(xu��)�c�Ԅe���P(gu��n)ϵ��
��2��ᘌ�(du��)�����{(di��o)���100���W(xu��)�����W(xu��)У�Q����ϲ�g��(gu��)�W(xu��)�����а��ӳ�ӵķ����S�C(j��)��ȡ6�˳�����(gu��)�W(xu��)�����M�������@6�������x2�����������M�ĽM�L(zh��ng)���O(sh��)�@������Ů���˔�(sh��)��![]() ����
����![]() �ķֲ��к͔�(sh��)�W(xu��)������
�ķֲ��к͔�(sh��)�W(xu��)������
������(sh��)��(j��)��
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
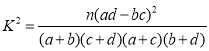 ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����λ��(sh��)![]() ��
��![]() ���鷴���������(sh��)����
���鷴���������(sh��)����![]() ��
��![]() ��
��![]() �քe��16��(g��)��12��(g��)����(sh��)������1�ͱ�������
�քe��16��(g��)��12��(g��)����(sh��)������1�ͱ�������![]() ���|(zh��)��(sh��)Ҳ��
���|(zh��)��(sh��)Ҳ��![]() ���|(zh��)��(sh��)����
���|(zh��)��(sh��)����![]() ���|(zh��)��(sh��)��
���|(zh��)��(sh��)��![]() ���|(zh��)��(sh��)��1��(g��)����
���|(zh��)��(sh��)��1��(g��)����![]() �����п���ֵ.
�����п���ֵ.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com