Question

已知平面直角坐標系中，A₁(-2，0)，A₂(2,0)、A₃(1,)，△A₁A₂A₃的外接圓為C；橢圓C₁以線段A₁A₂為長軸，離心率e=.

（1）求圓C及橢圓C₁的方程；

（2）設橢圓C₁的右焦點為F，點P為圓C上異于A₁、A₂的動點，過原點O作直線PF的垂線交直線x=2于點Q，判斷直線PQ與圓C的位置關系，并給出證明.

Answer 1

解:（1）∵|OA₁|=|OA₂|=|OA₃|=2,

∴外接圓C以原點O為圓心,線段OA₁為半徑.故其方程為x²+y²=4.

∴2a=4.∴a=2.又e=,∴c=,可得b=.

∴所求橢圓C₁的方程是+=1.

（2）直線PQ與圓C相切.證明：設P(x₀,y₀)(x₀≠±2),則y₀²=4-x₀².

當x₀=時,P(,±),Q(2,0),k_OP·k_PQ=-1,∴OP⊥PQ;

當x₀≠2時,k_PF=,∴k_OQ=.∴直線OQ的方程為y=x.

因此,點Q的坐標為(2,).

∵k_PQ==,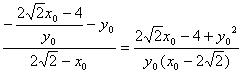

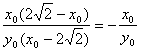∴當x₀=0時,k_PQ=0,OP⊥PQ;當x₀≠0時,k_OP=,

∴k_PQ·k_OP=-1,OP⊥PQ.綜上,當x≠±2時,OP⊥PQ,故直線PQ始終與圓C相切.