
(本題滿分12分)
設(shè) ,且
,且 滿足
滿足
(1)求 的值.
的值.
(2)求 的值.
的值.
(1)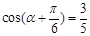 .(2)
.(2)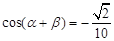 .
.
解析試題分析:(1)根據(jù)已知條件,將給出的方程組的每一個(gè)方程,利用化為單一函數(shù)的思想得到結(jié)論。
(2)經(jīng)過(guò)第一問(wèn)的求解,得到兩個(gè)關(guān)系式一個(gè)是角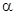 ,一個(gè)角
,一個(gè)角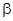 的三角函數(shù)式,然后整體構(gòu)造所求解的角,結(jié)合兩角和差的公式化簡(jiǎn)求值。
的三角函數(shù)式,然后整體構(gòu)造所求解的角,結(jié)合兩角和差的公式化簡(jiǎn)求值。
解:(1)∵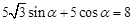 ,∴
,∴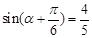 (3分)
(3分)
∵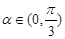 ,∴
,∴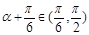 ,∴
,∴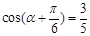 . (4分)
. (4分)
(2)又∵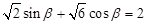 ,∴
,∴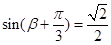 , (6分)
, (6分)
∵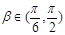 ,∴
,∴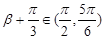 ,∴
,∴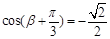 , (7分)
, (7分)
∴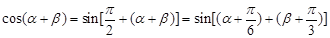
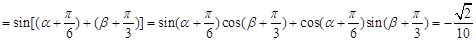
∴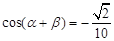 .
.
考點(diǎn):本試題主要考查了兩角和差的三角恒等變換的運(yùn)用。
點(diǎn)評(píng):解決該試題的關(guān)鍵是能夠根據(jù)已知條件整體的思想來(lái)構(gòu)造所求解的角,結(jié)合兩角和差的公式來(lái)得到,主義同角公式的平方關(guān)系的使用,確定出角的范圍,避免出現(xiàn)多解。


 小天才課時(shí)作業(yè)系列答案
小天才課時(shí)作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測(cè)驗(yàn)系列答案
黃岡小狀元滿分沖刺微測(cè)驗(yàn)系列答案 新輔教導(dǎo)學(xué)系列答案
新輔教導(dǎo)學(xué)系列答案 陽(yáng)光同學(xué)一線名師全優(yōu)好卷系列答案
陽(yáng)光同學(xué)一線名師全優(yōu)好卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)f(x)=2sinxcosx+cos2x(x∈R).
(1)求f(x)的最小正周期和最大值;
(2)若θ為銳角,且f(θ+ )=
)=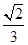 ,求tan2θ的值.
,求tan2θ的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分13分)已知函數(shù)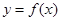
 .
.
(1)求函數(shù)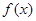 的最小正周期和最大值;
的最小正周期和最大值;
(2)在給出的直角坐標(biāo)系中,畫(huà)出函數(shù)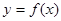 在區(qū)間
在區(qū)間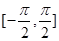 上的圖象.
上的圖象.
(3)設(shè)0<x<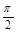 ,且方程
,且方程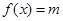 有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍.
有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本題滿分12 分)
已知
(Ⅰ)將 化成
化成 的形式;
的形式;
(Ⅱ)求 的最小正周期和最大值以及取得最大值時(shí)的
的最小正周期和最大值以及取得最大值時(shí)的 的值;
的值;
(Ⅲ)求  的單調(diào)遞增區(qū)間。
的單調(diào)遞增區(qū)間。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本題滿分14分)如圖,有一塊邊長(zhǎng)為1(百米)的正方形區(qū)域ABCD,在點(diǎn)A處有一個(gè)可轉(zhuǎn)動(dòng)的探照燈,其照射角 始終為
始終為 (其中點(diǎn)P,Q分別在邊BC,CD上),設(shè)
(其中點(diǎn)P,Q分別在邊BC,CD上),設(shè) .
.

(Ⅰ)用t表示出PQ的長(zhǎng)度,并探求 的周長(zhǎng)l是否為定值;
的周長(zhǎng)l是否為定值;
(Ⅱ)問(wèn)探照燈照射在正方形ABCD內(nèi)部區(qū)域陰影部分的面積S最大為多少(平方百米)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分14分)已知向量 ,
, ,設(shè)函數(shù)
,設(shè)函數(shù)
 的圖象關(guān)于直線
的圖象關(guān)于直線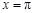 對(duì)稱,其中
對(duì)稱,其中 ,
, 為常數(shù),且
為常數(shù),且 .
.
(1)求函數(shù) 的最小正周期;
的最小正周期;
(2)若 的圖象經(jīng)過(guò)點(diǎn)
的圖象經(jīng)過(guò)點(diǎn) ,求函數(shù)
,求函數(shù) 在區(qū)間
在區(qū)間 上的取值范圍.
上的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)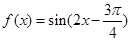 ,
,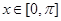
(Ⅰ)用“五點(diǎn)法”在所給的直角坐標(biāo)系中畫(huà)出函數(shù) 的圖像.
的圖像.
(Ⅱ)寫(xiě)出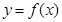 的圖象是由
的圖象是由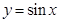 的圖象經(jīng)過(guò)怎樣的變換得到的.
的圖象經(jīng)過(guò)怎樣的變換得到的.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com