【題目】（1）已知雙曲線的中心在原點，焦點在x軸上，實軸長為4，漸近線方程為
．求雙曲線的標準方程；
（2）過（1）中雙曲線上一點P的直線分別交兩條漸近于
兩點，且P是線段AB的中點，求證：
為常數；
（3）我們知道函數
的圖象是由雙曲線
的圖象逆時針旋轉45°得到的，函數
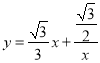的圖象也是雙曲線，請嘗試寫出曲線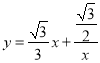的性質（不必證明）．
【答案】（1）
（2）證明見解析（3）詳見解析
【解析】
（1）根據雙曲線的性質求得雙曲線的方程；
（2）方法一：設A，B點坐標，求得P點坐標，代入雙曲線方程，即可求得
；
方法二：分類討論，設直線AB的方程，分別求得A和B點坐標，求得P點坐標，代入雙曲線方程，即可求得；
（3）根據曲線方程，分別求得曲線的性質．
（1）設雙曲線的方程為
，由
，
由雙曲線的漸近線方程為
，則
，則
，
∴雙曲線的方程為：；
（2）法一：由題不妨設
，則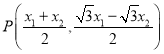
，
則P在雙曲線上，代入雙曲線方程得
法二：當直線AB的斜率不存在時，顯然
，則；
當直線AB的斜率存在時，設直線AB的方程為
則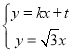
，則
，
同理
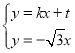，則
，
此時，
，代入雙曲線方程得
，則
（3）①對稱中心：原點，對稱軸方程：
，
②頂點坐標為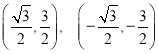
，焦點坐標：
，
，
實軸長：
，虛軸長：2b=2，焦距：2c=4；
③范圍：x≠0，
，
④漸近線：
．
科目：高中數學 來源： 題型：
【題目】如圖，在正方體ABCD-A1B1C1D1中，E，F分別是C1D1，CC1的中點，則異面直線AE與BF所成角的余弦值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市為了解游客人數的變化規律，提高旅游服務質量，收集并整理了2017年1月至2019年12月期間月接待游客量（單位：萬人）的數據，繪制了下面的折線圖．根據該折線圖，下列結論錯誤的是（ ）
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位數為30萬人
D.各年1月至6月的月接待游客量相對于7月至12月，波動性更小，變化比較平穩
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖①在直角梯形ABCP中，
，
，
，
，E，F，G分別是線段PC，PD，BC的中點，現將
折起，使平面
平面ABCD如圖②.
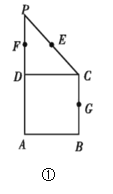
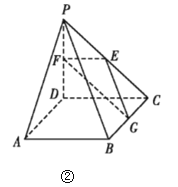
（1）求證:
平面EFG；
（2）求二面角G—EF—D的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
、
為雙曲線
的左、右焦點，過作垂直于
軸的直線，在軸上方交雙曲線
于點
，且
，圓
的方程是
.
（1）求雙曲線的方程；
（2）過雙曲線上任意一點
作該雙曲線兩條漸近線的垂線，垂足分別為
、
，求
的值；
（3）過圓上任意一點
作圓的切線
交雙曲線于
、
兩點，
中點為，求證：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，某地出土的一種“釘”是由四條線段組成，其結構能使它任意拋至水平面后，總有一端所在的直線豎直向上，并記組成該“釘”的四條線段的公共點為O，釘尖為
．
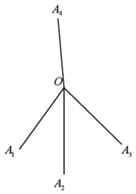
⑴設
，當
，
，
在同一水平面內時，求
與平面
所成角的大小
結果用反三角函數值表示
．
⑵若該“釘”的三個釘尖所確定的三角形的面積為
，要用某種線型材料復制100枚這種“釘”損耗忽略不計，共需要該種材料多少米？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于無窮數列
，若對任意
，滿足
且
（
是與
無關的常數），則稱數列為
數列.
（1）若
（），判斷數列是否為數列，說明理由；
（2）設
，求證：數列
是數列，并求常數的取值范圍；
（3）設數列
（，
），問數列
是否為數列？說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
