
【題目】設![]() 且
且![]() 恒成立.
恒成立.
(1)求實數![]() 的值;
的值;
(2)證明: ![]() 存在唯一的極大值點
存在唯一的極大值點![]() ,且
,且![]() .
.
【答案】(1)![]() ;(2)證明見解析
;(2)證明見解析
【解析】試題分析:(1)將問題轉化為![]() 恒成立的問題處理,分
恒成立的問題處理,分![]() 和
和![]() 兩種情況判斷即可;(2)由(1)得
兩種情況判斷即可;(2)由(1)得![]() ,故問題可轉化為
,故問題可轉化為![]() 有零點的問題,并進一步得到
有零點的問題,并進一步得到![]() 存在唯一的極大值點。然后根據函數的單調性可證得
存在唯一的極大值點。然后根據函數的單調性可證得![]() 。
。
試題解析:
(1)解:由條件知![]() 恒成立,
恒成立,
∵![]() ,
,
∴![]() 恒成立,
恒成立,
令![]() ,則
,則![]() 恒成立,
恒成立,
∴![]() ,
,
①當![]() 時,
時, ![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,
,
∴當![]() 時,
時, ![]() ,與
,與![]() 矛盾,不合題意。
矛盾,不合題意。
②當![]() 時,
時, ![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
∴ 當![]() 時,
時, ![]() 有極小值,也為最小值,且最小值為
有極小值,也為最小值,且最小值為![]() 。
。
又![]() 恒成立,
恒成立,
∴ ![]() ,
,
令![]()
則![]() ,
,
∴![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減,而
單調遞減,而![]() ,
,
所以由![]() 解得
解得![]() ,
,
綜上![]() .
.
(2)由條件得![]() ,
,
令![]() ,
,
所以![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增
單調遞增
又![]() ,
,
∴ ![]() ,
,
由零點存在定理及![]() 的單調性知,方程
的單調性知,方程![]() 在
在![]() 有唯一根,設為
有唯一根,設為![]() 且
且![]() ,
,
從而![]() 有兩個零點
有兩個零點![]() 和0,
和0,
所以![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
從而![]() 存在唯一的極大值點
存在唯一的極大值點![]() ,
,
由![]() 得
得![]() ,
,
∴![]()
![]() ,等號不成立,所以
,等號不成立,所以![]() ,
,
又![]() 在
在![]() 單調遞增,
單調遞增,
所以![]() ,
,
綜上可得![]() 成立.
成立.


科目:高中數學 來源: 題型:
【題目】如圖,斜率為1的直線過拋物線y2=2px(p>0)的焦點,與拋物線交于兩點A、B,M為拋物線 ![]() 上的動點.
上的動點. 
(1)若|AB|=8,求拋物線的方程;
(2)求S△ABM的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列{an},a1=1,an=an+12+2an+1(Ⅰ)求證:數列{log2(an+1)}為等比數列:
(Ⅱ)設bn=n1og2(an+1),數列{bn}的前n項和為Sn , 求證:1≤Sn<4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣ ![]() ﹣2lnx,a∈R.
﹣2lnx,a∈R.
(1)討論函數f(x)的單調性;
(2)若函數f(x)有兩個極值點x1 , x2 , 且x1<x2 , ①求a的取值范圍;
②證明:f(x2)<x2﹣1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A,B兩名同學在5次數學考試中的成績統計如下面的莖葉圖所示,若A,B兩人的平均成績分別是xA , xB , 觀察莖葉圖,下列結論正確的是( ) 
A.xA<xB , B比A成績穩定
B.xA>xB , B比A成績穩定
C.xA<xB , A比B成績穩定
D.xA>xB , A比B成績穩定
查看答案和解析>>
科目:高中數學 來源: 題型:
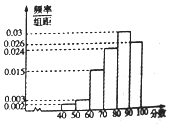
【題目】2017年3月14日,“ofo共享單車”終于來到蕪湖,ofo共享單車又被親切稱作“小黃車”是全球第一個無樁共享單車平臺,開創了首個“單車共享”模式.相關部門準備對該項目進行考核,考核的硬性指標是:市民對該項目的滿意指數不低于0.8,否則該項目需進行整改,該部門為了了解市民對該項目的滿意程度,隨機訪問了使用共享單車的100名市民,并根據這100名市民對該項目滿意程度的評分,繪制了如下頻率分布直方圖: (I)為了了解部分市民對“共享單車”評分較低的原因,該部門從評分低于60分的市民中隨機抽取2人進行座談,求這2人評分恰好都在[50,60)的概率;
(II)根據你所學的統計知識,判斷該項目能否通過考核,并說明理由.
(注:滿意指數= ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,集合A={x|﹣1<x<1},B={x|2≤4x≤8},C={x|a﹣4<x≤2a﹣7}.
(1)求(UA)∩B;
(2)若A∩C=C,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com