
【題目】函數 的圖象大致為( )
的圖象大致為( )
A.  B.
B. 
C.  D.
D. 
【答案】C
【解析】
由函數的解析式 ,當![]() 時,是函數的一個零點,屬于排除A,B,
時,是函數的一個零點,屬于排除A,B,
當x∈(0,1)時,cosx>0,![]() ,函數f(x) <0,函數的圖象在x軸下方,排除D.
,函數f(x) <0,函數的圖象在x軸下方,排除D.
本題選擇C選項.
點睛:函數圖象的識辨可從以下方面入手:(1)從函數的定義域,判斷圖象的左右位置;從函數的值域,判斷圖象的上下位置.(2)從函數的單調性,判斷圖象的變化趨勢.(3)從函數的奇偶性,判斷圖象的對稱性.(4)從函數的特征點,排除不合要求的圖象.利用上述方法排除、篩選選項.
【題型】單選題
【結束】
12
【題目】設![]() ,則
,則![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱臺ABCD﹣A1B1C1D1中,AA1⊥底面ABCD,四邊形ABCD為菱形,∠BAD=120°,AB=AA1=2A1B1=2. (Ⅰ)若M為CD中點,求證:AM⊥平面AA1B1B;
(Ⅱ)求直線DD1與平面A1BD所成角的正弦值.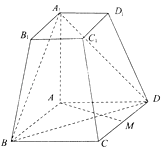
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知圓![]() 與
與![]() 軸的左右交點分別為
軸的左右交點分別為![]() ,與
,與![]() 軸正半軸的交點為
軸正半軸的交點為![]() .
.
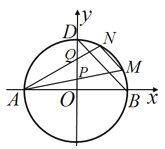
(1)若直線![]() 過點
過點![]() 并且與圓
并且與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若點![]() 是圓
是圓![]() 上第一象限內的點,直線
上第一象限內的點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,點
,點![]() 是線段
是線段![]() 的中點,直線
的中點,直線![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,AB是⊙O的直徑,VA 垂直于⊙O所在的平面,點C是圓周上不同于A,B的任意一點,M,N分別為VA,VC的中點,則下列結論正確的是( )

A. MN∥AB B. MN與BC所成的角為45°
C. OC⊥平面VAC D. 平面VAC⊥平面VBC
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+a|+|2x+1|,a∈R.
(1)當a=1時,求不等式f(x)≤1的解集;
(2)設關于x的不等式f(x)≤-2x+1的解集為P,且![]() P,求a的取值范圍.
P,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的左、右焦點分別為F1、F2 , 橢圓C過點P(1,
=1(a>b>0)的左、右焦點分別為F1、F2 , 橢圓C過點P(1, ![]() ),直線PF1交y軸于Q,且
),直線PF1交y軸于Q,且 ![]() =2
=2 ![]() ,O為坐標原點.
,O為坐標原點.
(1)求橢圓C的方程;
(2)設M是橢圓C的上頂點,過點M分別作直線MA,MB交橢圓C于A,B兩點,設這兩條直線的斜率分別為k1 , k2 , 且k1+k2=2,證明:直線AB過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(1,2),過點P(5,﹣2)的直線與拋物線y2=4x相交于B,C兩點,則△ABC是( )
A.直角三角形
B.鈍角三角形
C.銳角三角形
D.不能確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖像是由函數
的圖像是由函數![]() 的圖像經如下變換得到:先將
的圖像經如下變換得到:先將![]() 圖像上所有點的縱坐標伸長到原來的2倍(橫坐標不變),再將所得到的圖像向右平移
圖像上所有點的縱坐標伸長到原來的2倍(橫坐標不變),再將所得到的圖像向右平移![]() 個單位長度.
個單位長度.
(Ⅰ)求函數![]() 的解析式,并求其圖像的對稱軸方程;
的解析式,并求其圖像的對稱軸方程;
(Ⅱ)已知關于![]() 的方程
的方程![]() 在
在![]() 內有兩個不同的解
內有兩個不同的解![]() .
.
(1)求實數m的取值范圍;
(2)證明:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列判斷錯誤的是
A. 若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ;
;
B. 若![]() 組數據
組數據![]() 的散點都在
的散點都在![]() 上,則相關系數
上,則相關系數![]() ;
;
C. 若隨機變量![]() 服從二項分布:
服從二項分布: ![]() , 則
, 則![]() ;
;
D. ![]() 是
是![]() 的充分不必要條件;
的充分不必要條件;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com