
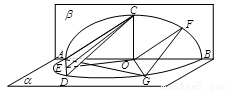
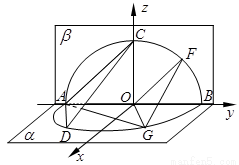
如圖1,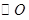 的直徑AB=4,點(diǎn)C、D為
的直徑AB=4,點(diǎn)C、D為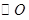 上兩點(diǎn),且
上兩點(diǎn),且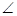 CAB=45°,
CAB=45°,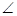 DAB=60°,F(xiàn)為弧BC的中點(diǎn).沿直徑AB折起,使兩個(gè)半圓所在平面互相垂直,如圖2.
DAB=60°,F(xiàn)為弧BC的中點(diǎn).沿直徑AB折起,使兩個(gè)半圓所在平面互相垂直,如圖2.
(I)求證:OF 平面ACD;
平面ACD;
(Ⅱ)求二面角C—AD—B的余弦值;
(Ⅲ)在弧BD上是否存在點(diǎn)G,使得FG 平面ACD?若存在,試指出點(diǎn)G的位置;若不存在,請(qǐng)說(shuō)明理由.
平面ACD?若存在,試指出點(diǎn)G的位置;若不存在,請(qǐng)說(shuō)明理由.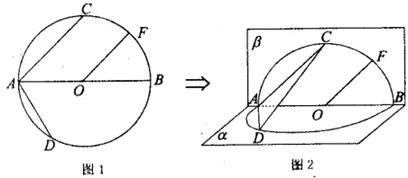
(1)對(duì)于線面平行的判定關(guān)鍵是證明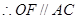 來(lái)得到。
來(lái)得到。
(2)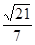
(3) 在弧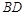 上存在點(diǎn)
上存在點(diǎn)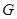 ,使得
,使得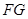 //平面
//平面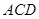 ,且點(diǎn)
,且點(diǎn)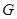 為弧
為弧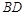 的中點(diǎn)
的中點(diǎn)
【解析】
試題分析:(方法一):證明:(Ⅰ)如右圖,連接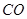 ,
,
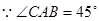 ,
, . …1分
又
. …1分
又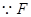 為弧
為弧 的中點(diǎn),
的中點(diǎn),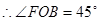 ,
,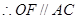 .
.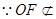 平面
平面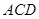 ,
, 平面
平面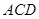 ,
,
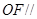 平面
平面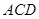 . …4分
. …4分
解:(Ⅱ)過(guò) 作
作 于
于 ,連
,連 .
.
 ,平面
,平面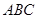 ⊥平面
⊥平面 .
.
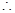
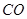 ⊥平面
⊥平面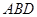 .又
.又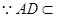 平面
平面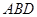 ,
, 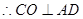 ,
, 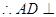 平面
平面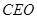 ,
,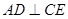 ,則∠
,則∠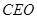 是二面角
是二面角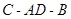 的平面角.
的平面角. 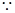
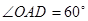 ,
,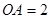 ,
, 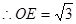 . 由
. 由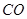 ⊥平面
⊥平面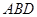 ,
,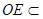 平面
平面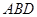 ,得
,得 為直角三角形,
為直角三角形,
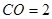 ,
,
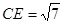
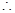
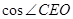 =
=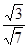 =
=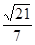 . 8分
. 8分
(Ⅲ)取弧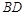 的中點(diǎn)
的中點(diǎn)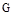 ,連結(jié)
,連結(jié) 、
、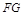 ,則
,則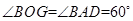
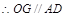 …
…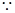
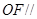 平面
平面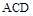 ,
,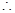 平面
平面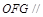 平面
平面
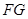 //平面
//平面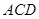 .
.
因此,在弧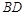 上存在點(diǎn)
上存在點(diǎn)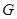 ,使得
,使得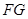 //平面
//平面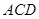 ,且點(diǎn)
,且點(diǎn)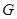 為弧
為弧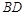 的中點(diǎn).…12分
的中點(diǎn).…12分
(方法二):證明:(Ⅰ)如圖,以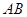 所在的直線為
所在的直線為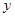 軸,以
軸,以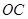 所在的直線為
所在的直線為 軸,以
軸,以 為原點(diǎn),建立空間直角坐標(biāo)系
為原點(diǎn),建立空間直角坐標(biāo)系
則
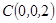 .…… 1分
.…… 1分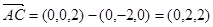 ,
,
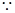 點(diǎn)
點(diǎn) 為弧
為弧 的中點(diǎn),
的中點(diǎn),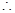 點(diǎn)
點(diǎn)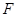 的坐標(biāo)為
的坐標(biāo)為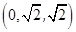 ,
,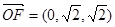 .
.
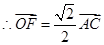 解:(Ⅱ)
解:(Ⅱ) ,
, 點(diǎn)
點(diǎn)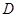 的坐標(biāo)
的坐標(biāo)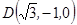 ,
,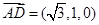 .
.
設(shè)二面角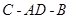 的大小為
的大小為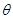 ,
,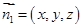 為平面
為平面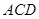 的一個(gè)法向量.
的一個(gè)法向量.
由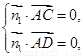 有
有 即
即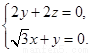
取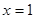 ,解得
,解得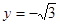 ,
,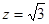 .
. 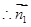 =
=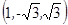 . 5分
. 5分
取平面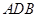 的一個(gè)法向量
的一個(gè)法向量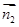 =
=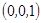 , 6分
, 6分
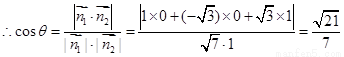 . 8分
. 8分
(Ⅲ)設(shè)在弧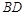 上存在點(diǎn)
上存在點(diǎn)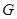
 ,
,
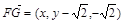 ,由(Ⅱ)知平面
,由(Ⅱ)知平面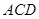 的一個(gè)法向量為
的一個(gè)法向量為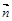 =
=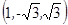 .
.
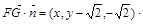
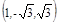 =
=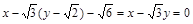 ① 9分
① 9分
又因?yàn)?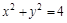 ②由①②兩式聯(lián)立解得
②由①②兩式聯(lián)立解得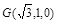 ,…11分
,…11分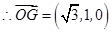 ,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013080812364422298371/SYS201308081237211004650232_DA.files/image065.png">,所以
,因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013080812364422298371/SYS201308081237211004650232_DA.files/image065.png">,所以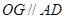 ,則
,則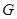 為弧
為弧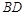 的中點(diǎn),因此,在弧
的中點(diǎn),因此,在弧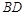 上存在點(diǎn)
上存在點(diǎn)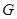 ,使得
,使得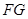 //平面
//平面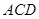 ,且點(diǎn)
,且點(diǎn)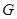 為弧
為弧 的中點(diǎn). ………12分
的中點(diǎn). ………12分
考點(diǎn):線面平行和二面角的平面角
點(diǎn)評(píng):主要是考查了二面角的求解,以及線面平行 的判定定理的運(yùn)用,屬于基礎(chǔ)題。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 選做題(考生只能從A、B、C題中選作一題)
選做題(考生只能從A、B、C題中選作一題)
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
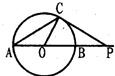
 如圖,⊙O的直徑AB的延長(zhǎng)線與弦CD的延長(zhǎng)線相交于點(diǎn)P,E為⊙O上一點(diǎn),AE=AC,DE交AB于點(diǎn)F.
如圖,⊙O的直徑AB的延長(zhǎng)線與弦CD的延長(zhǎng)線相交于點(diǎn)P,E為⊙O上一點(diǎn),AE=AC,DE交AB于點(diǎn)F.查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 【選做題】在A,B,C,D四小題中只能選做2題,每小題10分,共計(jì)20分.請(qǐng)?jiān)诖痤}卡指定區(qū)域內(nèi)作答.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.
【選做題】在A,B,C,D四小題中只能選做2題,每小題10分,共計(jì)20分.請(qǐng)?jiān)诖痤}卡指定區(qū)域內(nèi)作答.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.
|
| π |
| 4 |
| 2 |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 (2012•鹽城三模)選修4-1:幾何證明選講:
(2012•鹽城三模)選修4-1:幾何證明選講: |
| AE |
 |
| AC |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com