
【題目】已知函數![]() ,
, ![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的值域;
的值域;
(2)如果對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)是否存在實數![]() ,使得函數
,使得函數![]() 的最大值為0,若存在,求出
的最大值為0,若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
【答案】(1)[0,2];(2)(-∞,![]() );(3)答案見解析.
);(3)答案見解析.
【解析】試題分析:(1)由h(x)=-2(log3x-1)2+2,根據log3x∈[0,2],即可得值域;
(2)由![]() ,令t=log3x,因為x∈[1,9],所以t=log3x∈[0,2],得(3-4t)(3-t)>k對一切t∈[0,2]恒成立,利用二次函數求函數的最小值即可;
,令t=log3x,因為x∈[1,9],所以t=log3x∈[0,2],得(3-4t)(3-t)>k對一切t∈[0,2]恒成立,利用二次函數求函數的最小值即可;
(3)由![]() ,假設最大值為0,因為
,假設最大值為0,因為![]() ,則有
,則有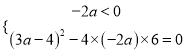 ,求解即可.
,求解即可.
試題解析:
(1)h(x)=(4-2log3x)·log3x=-2(log3x-1)2+2,
因為x∈[1,9],所以log3x∈[0,2],
故函數h(x)的值域為[0,2].
(2)由![]() ,
,
得(3-4log3x)(3-log3x)>k,
令t=log3x,因為x∈[1,9],所以t=log3x∈[0,2],
所以(3-4t)(3-t)>k對一切t∈[0,2]恒成立,
令![]() ,其對稱軸為
,其對稱軸為![]() ,
,
所以當![]() 時,
時, ![]() 的最小值為
的最小值為![]() ,
,
綜上,實數k的取值范圍為(-∞,![]() )..
)..
(3)假設存在實數![]() ,使得函數
,使得函數![]() 的最大值為0,
的最大值為0,
由![]() .
.
因為![]() ,則有
,則有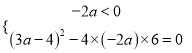 ,解得
,解得![]() ,所以不存在實數
,所以不存在實數![]() ,
,
使得函數![]() 的最大值為0.
的最大值為0.


 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:
【題目】已知直線l過點P(-1,2)且與兩坐標軸的正半軸所圍成的三角形面積等于![]() .
.
(1)求直線l的方程.
(2)求圓心在直線l上且經過點M(2,1),N(4,-1)的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,若方程f(x)=a有四個不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 則x3(x1+x2)+
,若方程f(x)=a有四個不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 則x3(x1+x2)+ ![]() 的取值范圍是( )
的取值范圍是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為提升學生的英語學習能力,進行了主題分別為“聽”、“說”、“讀”、“寫”四場競賽.規定:每場競賽的前三名得分分別為![]() ,
, ![]() ,
, ![]() (
(![]() ,且
,且![]() ,
, ![]() ,
, ![]() ),選手的最終得分為各場得分之和.最終甲、乙、丙三人包攬了每場競賽的前三名,在四場競賽中,已知甲最終分為
),選手的最終得分為各場得分之和.最終甲、乙、丙三人包攬了每場競賽的前三名,在四場競賽中,已知甲最終分為![]() 分,乙最終得分為
分,乙最終得分為![]() 分,丙最終得分為
分,丙最終得分為![]() 分,且乙在“聽”這場競賽中獲得了第一名,則“聽”這場競賽的第三名是( )
分,且乙在“聽”這場競賽中獲得了第一名,則“聽”這場競賽的第三名是( )
A. 甲 B. 乙 C. 丙 D. 甲和丙都有可能
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() 為兩條不同的直線,
為兩條不同的直線, ![]() ,
, ![]() 為兩個不同的平面,對于下列四個命題:
為兩個不同的平面,對于下列四個命題:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正確命題的個數有( )
A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com