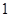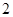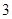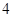如圖,在正三棱柱ABC—A
1B
1C
1中,底面邊長及側(cè)棱長均為2,D是棱AB的中點,
(1)求證
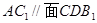
;
(2)求異面直線AC
1與B
1C所成角的余弦值.

(1)略;(2)
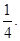
(1)連接
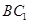
與
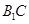
,交點為
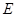
,則
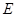
是
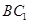
的中點,又D是棱AB的中點,所以
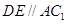
,根據(jù)線面平行的判定定理可證出
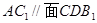
;
(2)由(1)得
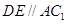
,所以異面直線AC
1與B
1C所成的角就是
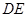
與
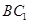
所成的角或其補角,在
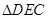
中,
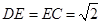
,

,根據(jù)余弦定理求出異面直線AC
1與B
1C所成角的余弦值.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,底面為直角梯形的四棱錐

中,AD∥BC,
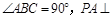
平面

,

,BC=6.
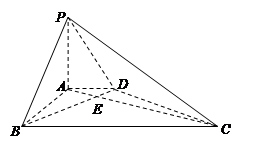
(Ⅰ)求證:BD⊥平面PAC;
(Ⅱ)求二面角

的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,已知四棱錐
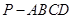
的底面是正方形,
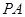
⊥底面
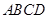
,且
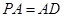
,點
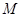
、
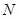
分別為側(cè)棱
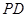
、
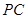
的中點
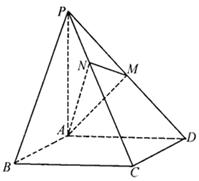
(1)求證:
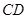
∥平面
;
(2)求證:
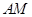
⊥平面
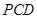
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
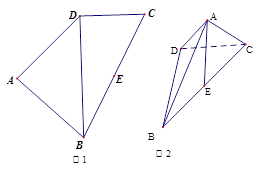
如圖,四邊形

中(圖1),
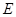
是
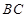
的中點,
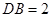
,
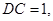
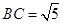
,
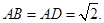
將(圖1)沿直線
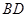
折起,使二面角
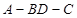
為

(如圖2)
(1)求證:

平面
;
(2)求二面角A—DC—B的余弦值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(14分)如圖①,直角梯形
中,
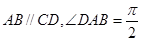
,點
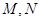
分別在
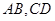
上,且
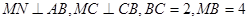
,現(xiàn)將梯形
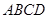
A沿
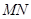
折起,使平面
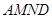
與平面
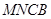
垂直(如圖②).
(1)求證:
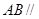
平面
;
(2)當

時,求二面角
的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設(shè)
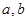
是兩條直線,
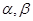
是兩個平面,則下列4組條件中:①
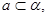
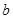
∥

,
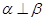
;②
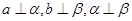
;③
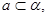
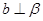
,
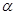
∥

;④
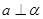
,
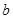
∥

,
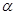
∥

。
能推得
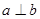
的條件有( )組。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
下列說法中:①平行于同一條直線的兩個平面平行;②平行于同一平面的兩個平面平行;③垂直于同一條直線的兩條直線平行;④垂直于同一平面的兩條直線平行.其中正確的說法個數(shù)為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知兩條相交直線
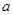
,
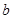
,
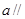
平面
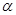
,則
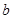
與
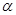
的位置關(guān)系是( )
查看答案和解析>>

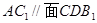 ;
;
 中(圖1),
中(圖1),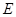 是
是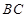 的中點,
的中點,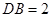 ,
,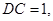
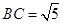 ,
,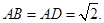 將(圖1)沿直線
將(圖1)沿直線 折起,使二面角
折起,使二面角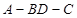 為
為 (如圖2)
(如圖2) 平面
平面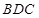 ;
;
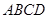 中,
中,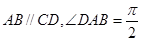 ,點
,點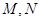 分別在
分別在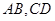 上,且
上,且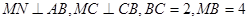 ,現(xiàn)將梯形
,現(xiàn)將梯形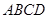 A沿
A沿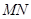 折起,使平面
折起,使平面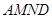 與平面
與平面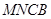 垂直(如圖②).
垂直(如圖②).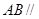 平面
平面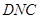 ;
; 時,求二面角
時,求二面角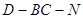 的大小.
的大小.