
【題目】過橢圓![]() 的左頂點
的左頂點![]() 作斜率為2的直線,與橢圓的另一個交點為
作斜率為2的直線,與橢圓的另一個交點為![]() ,與
,與![]() 軸的交點為
軸的交點為![]() ,已知
,已知![]() .
.
(1)求橢圓的離心率;
(2)設動直線![]() 與橢圓有且只有一個公共點
與橢圓有且只有一個公共點![]() ,且與直線
,且與直線![]() 相交于點
相交于點![]() ,若
,若![]() 軸上存在一定點
軸上存在一定點![]() ,使得
,使得![]() ,求橢圓的方程.
,求橢圓的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(I)根據![]()
![]() ,設直線方程為
,設直線方程為![]() ,
,![]()
確定![]() 的坐標,由
的坐標,由![]() 確定得到
確定得到![]() ,
,
再根據![]() 點在橢圓上,求得
點在橢圓上,求得![]() 進一步即得所求
進一步即得所求![]() ;
;
(2)由![]() 可設
可設![]() ,
,
得到橢圓的方程為![]() ,
,
由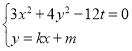 得
得![]()
根據動直線![]() 與橢圓有且只有一個公共點P
與橢圓有且只有一個公共點P
得到![]() ,整理得
,整理得![]() .
.
確定![]() 的坐標
的坐標![]() ,
,
又![]() ,
, ![]()
![]()
若![]() 軸上存在一定點
軸上存在一定點![]() ,使得
,使得![]() ,那么
,那么![]()
可得![]() ,由
,由![]() 恒成立,故
恒成立,故![]() ,得解.
,得解.
試題解析:(1)∵![]()
![]() ,設直線方程為
,設直線方程為![]() ,
,![]()
令![]() ,則
,則![]() ,∴
,∴![]() , 2分
, 2分
∴![]() 3分
3分
∵![]() ,∴
,∴![]() =
=![]() ,
,
整理得![]() 4分
4分
∵![]() 點在橢圓上,∴
點在橢圓上,∴![]() ,∴
,∴![]() 5分
5分
∴![]() 即
即![]() ,∴
,∴![]() 6分
6分
(2)∵![]() 可設
可設![]() ,
,
∴橢圓的方程為![]() 7分
7分
由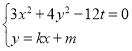 得
得![]() 8分
8分
∵動直線![]() 與橢圓有且只有一個公共點P
與橢圓有且只有一個公共點P
∴![]() ,即
,即![]()
整理得![]() 9分
9分
設![]()
![]() 則有
則有![]() ,
,![]()
∴![]() 10分
10分
又![]() ,
,![]()
![]()
若![]() 軸上存在一定點
軸上存在一定點![]() ,使得
,使得![]() ,
,
∴![]() 恒成立
恒成立
整理得![]() , 12分
, 12分
∴![]() 恒成立,故
恒成立,故![]()
所求橢圓方程為![]() 13分
13分


 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)設![]() 為
為![]() 上的一點,滿足
上的一點,滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了響應教育部頒布的《關于推進中小學生研學旅行的意見》,某校計劃開設八門研學旅行課程,并對全校學生的選課意向進行調查(調查要求全員參與,每個學生必須從八門課程中選出唯一一門課程).本次調查結果如下.
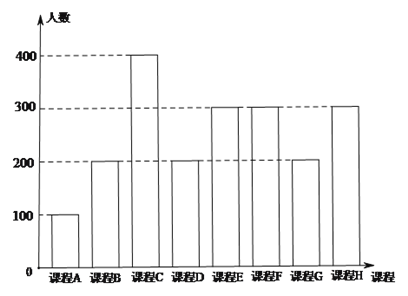
圖中,課程![]() 為人文類課程,課程
為人文類課程,課程![]() 為自然科學類課程.為進一步研究學生選課意向,結合上面圖表,采取分層抽樣方法從全校抽取1%的學生作為研究樣本組(以下簡稱“組
為自然科學類課程.為進一步研究學生選課意向,結合上面圖表,采取分層抽樣方法從全校抽取1%的學生作為研究樣本組(以下簡稱“組![]() ”).
”).
(Ⅰ)在“組![]() ”中,選擇人文類課程和自然科學類課程的人數各有多少?
”中,選擇人文類課程和自然科學類課程的人數各有多少?
(Ⅱ)某地舉辦自然科學營活動,學校要求:參加活動的學生只能是“組![]() ”中選擇
”中選擇![]() 課
課
程或![]() 課程的同學,并且這些同學以自愿報名繳費的方式參加活動. 選擇
課程的同學,并且這些同學以自愿報名繳費的方式參加活動. 選擇![]() 課程的學生中有
課程的學生中有![]() 人參加科學營活動,每人需繳納
人參加科學營活動,每人需繳納![]() 元,選擇
元,選擇![]() 課程的學生中有
課程的學生中有![]() 人參加該活動,每人需繳納
人參加該活動,每人需繳納![]() 元.記選擇
元.記選擇![]() 課程和
課程和![]() 課程的學生自愿報名人數的情況為
課程的學生自愿報名人數的情況為![]() ,參加活動的學生繳納費用總和為
,參加活動的學生繳納費用總和為![]() 元.
元.
①當![]() 時,寫出
時,寫出![]() 的所有可能取值;
的所有可能取值;
②若選擇![]() 課程的同學都參加科學營活動,求
課程的同學都參加科學營活動,求![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
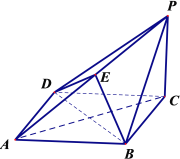
【題目】如圖,在四棱錐![]() 中, 底面
中, 底面![]() 為菱形,
為菱形,![]() 平面
平面![]() ,點
,點![]() 在棱
在棱![]() 上.
上.
(Ⅰ)求證:直線![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求證:
,求證:![]() ;
;
(Ⅲ)是否存在點![]() ,使得四面體
,使得四面體![]() 的體積等于四面體
的體積等于四面體![]() 的體積的
的體積的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )與
)與![]() 軸交于
軸交于![]() ,
, ![]() 兩點,
兩點, ![]() 為橢圓
為橢圓![]() 的左焦點,且
的左焦點,且![]() 是邊長為2的等邊三角形.
是邊長為2的等邊三角形.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() (
(![]() 與
與![]() 不重合),則直線
不重合),則直線![]() 與
與![]() 軸交于點
軸交于點![]() ,求
,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據如圖給出的2004年至2013年我國二氧化硫年排放量(單位:萬噸)柱形圖,以下結論中不正確的是( ) 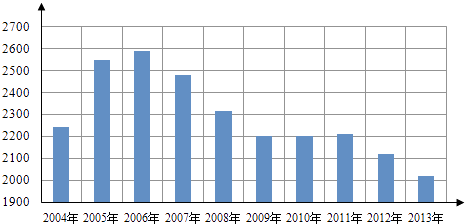
A.逐年比較,2008年減少二氧化硫排放量的效果最顯著
B.2007年我國治理二氧化硫排放顯現成效
C.2006年以來我國二氧化硫年排放量呈減少趨勢
D.2006年以來我國二氧化硫年排放量與年份正相關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我校舉行的 “青年歌手大選賽”吸引了眾多有才華的學生參賽.為了了解本次比賽成績情況,從中抽取了50名學生的成績(得分取正整數,滿分為100分)作為樣本進行統計.請根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
![]()
組別 | 分組 | 頻數 | 頻率 |
第1組 | [50,60) | 8 | 0.16 |
第2組 | [60,70) | a | ▓ |
第3組 | [70,80) | 20 | 0.40 |
第4組 | [80,90) | ▓ | 0.08 |
第5組 | [90,100] | 2 | b |
合計 | ▓ | ▓ |
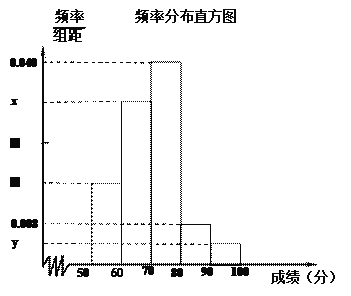
(1)求出![]() 的值;
的值;
(2)在選取的樣本中,從成績是80分以上(含80分)的同學中隨機抽取2名同學參加元旦晚會,求所抽取的2名同學中至少有1名同學來自第5組的概率;
(3)根據頻率分布直方圖,估計這50名學生成績的眾數、中位數和平均數。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com