
【題目】如圖,點A的坐標為(﹣8,0),點P的坐標為 ![]() ,直線y=
,直線y= ![]() x+b過點A,交y軸于點B,以點P為圓心,以PA為半徑的圓交x軸于點C.
x+b過點A,交y軸于點B,以點P為圓心,以PA為半徑的圓交x軸于點C.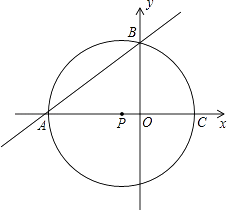
(1)判斷點B是否在⊙P上?說明理由.
(2)求過A、B、C三點的拋物線的解析式;并求拋物線與⊙P另外一個交點為D的坐標.
(3)⊙P上是否存在一點Q,使以A、P、B、Q為頂點的四邊形是菱形?若存在,求出點Q的坐標;若不存在,請說明理由.
【答案】
(1)
解:∵A(﹣8,0)在直線y= ![]() x+b上,則有b=6,
x+b上,則有b=6,
∴點B(0,6),即OB=6,
在Rt△BOP中,由勾股定理得PB= ![]() ,則PB=PA,
,則PB=PA,
∴點B在⊙P上
(2)
解:AC=2PA= ![]() ,則OC=
,則OC= ![]() ,點C
,點C ![]() ,
,
拋物線過點A、C,則設所求拋物線為y=a(x+8)(x﹣ ![]() ),代入點C
),代入點C ![]() ,則有a=
,則有a= ![]() ,
,
拋物線的解析式為y=﹣ ![]() x2﹣
x2﹣ ![]() x+6,
x+6,
直線x= ![]() 是拋物線和圓P的對稱軸,點B的對稱點為D,由對稱可得D
是拋物線和圓P的對稱軸,點B的對稱點為D,由對稱可得D ![]()
(3)
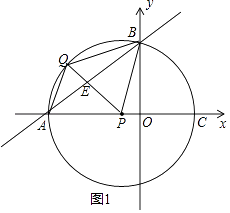
解:當點Q在⊙P上時,有PQ=PA= ![]() ,
,
如圖1所示,假設AB為菱形的對角線,那么PQ⊥AB且互相平分,由勾股定理得PE= ![]() ,則2PE≠PQ,所以四邊形APBQ不是菱形.
,則2PE≠PQ,所以四邊形APBQ不是菱形.
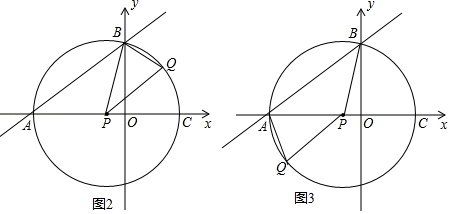
如圖2所示,假設AB、AP為菱形的鄰邊,則AB≠AP,所以四邊形APQB不是菱形.
如圖3所示,假設 AB、BP為菱形的鄰邊,則AB≠BP,所以四邊形AQPB不是菱形.
綜上所述,⊙P上不存在點Q,使以A、P、B、Q為頂點的四邊形.
【解析】(1)把A(﹣8,0)代入y= ![]() x+b得到點B(0,6),即OB=6,根據勾股定理即可得到結論;(2)AC=2PA=
x+b得到點B(0,6),即OB=6,根據勾股定理即可得到結論;(2)AC=2PA= ![]() ,則OC=
,則OC= ![]() ,點C
,點C ![]() ,得到拋物線的解析式為y=﹣
,得到拋物線的解析式為y=﹣ ![]() x2﹣
x2﹣ ![]() x+6,直線x=
x+6,直線x= ![]() 是拋物線和圓P的對稱軸,于是得到結論;(3)當點Q在⊙P上時,有PQ=PA=
是拋物線和圓P的對稱軸,于是得到結論;(3)當點Q在⊙P上時,有PQ=PA= ![]() ,如圖1所示,假設AB為菱形的對角線,如圖2所示,假設AB、AP為菱形的鄰邊,如圖3所示,假設 AB、BP為菱形的鄰邊,于是得到結論.
,如圖1所示,假設AB為菱形的對角線,如圖2所示,假設AB、AP為菱形的鄰邊,如圖3所示,假設 AB、BP為菱形的鄰邊,于是得到結論.
【考點精析】掌握勾股定理的概念是解答本題的根本,需要知道直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2.


科目:初中數學 來源: 題型:
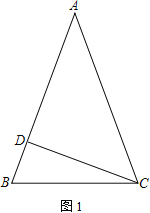
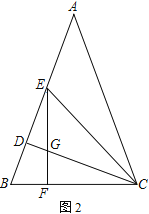
【題目】在△ABC中,AB=AC,CD為AB邊上的高
(1) 如圖1,求證:∠BAC=2∠BCD
(2) 如圖2,∠ACD的平分線CE交AB于E,過E作EF⊥BC于F,EF與CD交于點G.若ED=m,BD=n,請用含有m、n的代數式表示△EGC的面積
查看答案和解析>>
科目:初中數學 來源: 題型:
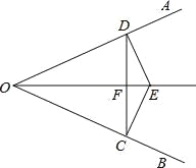
【題目】如圖,已知:E 是∠AOB 的平分線上一點,EC⊥OB,ED⊥OA,C、D是垂足,連接 CD,且交 OE 于點F.
(1)求證:OD=OC;
(2)求證:OE 是 CD 的垂直平分線;
(3)若∠AOB=60°,請你探究 OE,EF 之間有什么數量關系?并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)(﹣12a2b2c)(﹣![]() abc2)2=___________;
abc2)2=___________;
(2)(3a2b﹣4ab2﹣5ab﹣1)(﹣2ab2)=___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年10月17日是我國第五個“扶貧日”,某校學生會干部對學生倡導的“扶貧”自愿捐款活動進行抽樣調查,得到一組學生捐款情況的數據,對學校部分捐款人數進行調查和分組統計后,將數據整理成如圖所示的統計圖,(圖中信息不完整),已知A.B兩組捐款人數的比為1:5.
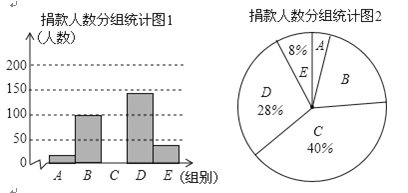
被調查的捐款人數分組統計表:
組別 | 捐款額x/元 | 人數 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
請結合以上信息解答下列問題:
(1)求a的值和參與調查的總人數;
(2)補全“被調查的捐款人數分組統計圖1”并計算扇形B的圓心角度數;
(3)已知該校有學生2200人,請估計捐款數不少于30元的學生人數有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等,經洽談,甲商場優惠方案是:每購買十套隊服,送一個足球;乙商場優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)求每套隊服和每個足球的價格是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所花的費用;
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
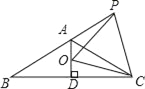
【題目】如圖,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于點D,點P是BA延長線上一點,點O是線段AD上一點,OP=OC.
(1)求∠APO+∠DCO的度數;
(2)求證:點P在OC的垂直平分線上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com