
【題目】如圖,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中點,點E在邊AC上,將△ADE沿DE翻折,使得點A落在點A'處,當A'E⊥AC時,A'B= . 
【答案】![]() 或7
或7 ![]()
【解析】解:分兩種情況: ①如圖1,過D作DG⊥BC與G,交A′E與F,過B作BH⊥A′E與H,
∵D為AB的中點,
∴BD= ![]() AB=AD,
AB=AD,
∵∠C=90,AC=8,BC=6,
∴AB=10,
∴BD=AD=5,
sin∠ABC= ![]() ,
,
∴ ![]() ,
,
∴DG=4,
由翻折得:∠DA′E=∠A,A′D=AD=5,
∴sin∠DA′E=sin∠A= ![]() ,
,
∴ ![]() ,
,
∴DF=3,
∴FG=4﹣3=1,
∵A′E⊥AC,BC⊥AC,
∴A′E∥BC,
∴∠HFG+∠DGB=180°,
∵∠DGB=90°,
∴∠HFG=90°,
∵∠EHB=90°,
∴四邊形HFGB是矩形,
∴BH=FG=1,
同理得:A′E=AE=8﹣1=7,
∴A′H=A′E﹣EH=7﹣6=1,
在Rt△AHB中,由勾股定理得:A′B= ![]() =
= ![]() ;
;
②如圖2,過D作MN∥AC,交BC與于N,過A′作A′F∥AC,交BC的延長線于F,延長A′E交直線DN于M,
∵A′E⊥AC,
∴A′M⊥MN,A′E⊥A′F,
∴∠M=∠MA′F=90°,
∵∠ACB=90°,
∴∠F=∠ACB=90°,
∴四邊形MA′FN是矩形,
∴MN=A′F,FN=A′M,
由翻折得:A′D=AD=5,
Rt△A′MD中,∴DM=3,A′M=4,
∴FN=A′M=4,
Rt△BDN中,∵BD=5,
∴DN=4,BN=3,
∴A′F=MN=DM+DN=3+4=7,
BF=BN+FN=3+4=7,
Rt△ABF中,由勾股定理得:A′B= ![]() =7
=7 ![]() ;
;
綜上所述,A′B的長為 ![]() 或7
或7 ![]() .
.
故答案為: ![]() 或7
或7 ![]() .
.
分兩種情況:
①如圖1,作輔助線,構建矩形,先由勾股定理求斜邊AB=10,由中點的定義求出AD和BD的長,證明四邊形HFGB是矩形,根據同角的三角函數列式可以求DG和DF的長,并由翻折的性質得:∠DA′E=∠A,A′D=AD=5,由矩形性質和勾股定理可以得出結論:A′B= ![]() ;②如圖2,作輔助線,構建矩形A′MNF,同理可以求出A′B的長.
;②如圖2,作輔助線,構建矩形A′MNF,同理可以求出A′B的長.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知點A(0,4),B(2,0).
(1)求直線AB的函數解析式;
(2)已知點M是線段AB上一動點(不與點A、B重合),以M為頂點的拋物線y=(x﹣m)2+n與線段OA交于點C.
①求線段AC的長;(用含m的式子表示)
②是否存在某一時刻,使得△ACM與△AMO相似?若存在,求出此時m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察等式:① ![]() =1﹣
=1﹣ ![]() ;②
;② ![]() =
= ![]() ﹣
﹣ ![]() ;③
;③ ![]() =
= ![]() ﹣
﹣ ![]() ;④
;④ ![]() =
= ![]() ﹣
﹣ ![]() ,…
,…
(1)試用字母n的等式表示出你發現的規律,并證明該等式成立;
(2)![]()
+ ![]() +
+ ![]() +…+
+…+ ![]() = . (直接寫出結果)
= . (直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數 ![]() ,下列結論錯誤的是( )
,下列結論錯誤的是( )
A.圖象經過點(1,1)
B.當x<0時,y隨著x的增大而增大
C.當x>1時,0<y<1
D.圖象在第一、三象限
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】反比例函數y= ![]() (a>0,a為常數)和y=
(a>0,a為常數)和y= ![]() 在第一象限內的圖象如圖所示,點M在y=
在第一象限內的圖象如圖所示,點M在y= ![]() 的圖象上,MC⊥x軸于點C,交y=
的圖象上,MC⊥x軸于點C,交y= ![]() 的圖象于點A;MD⊥y軸于點D,交y=
的圖象于點A;MD⊥y軸于點D,交y= ![]() 的圖象于點B,當點M在y=
的圖象于點B,當點M在y= ![]() 的圖象上運動時,以下結論:①S△ODB=S△OCA;②四邊形OAMB的面積不變;③當點A是MC的中點時,則點B是MD的中點.其中正確結論的序號是 .
的圖象上運動時,以下結論:①S△ODB=S△OCA;②四邊形OAMB的面積不變;③當點A是MC的中點時,則點B是MD的中點.其中正確結論的序號是 . 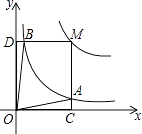
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A(n,﹣2),B(1,4)是一次函數y=kx+b的圖象和反比例函數y= ![]() 的圖象的兩個交點,直線AB與y軸交于點C.
的圖象的兩個交點,直線AB與y軸交于點C. 
(1)求反比例函數和一次函數的關系式;
(2)求△AOC的面積;
(3)結合圖象直接寫出不等式kx+b< ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊AB=20,面積為320,∠BAD<90°,⊙O與邊AB,AD都相切,AO=10,則⊙O的半徑長等于( ) 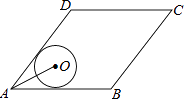
A.5
B.6
C.2 ![]()
D.3 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com