
【題目】一個等腰三角形的兩邊長為3和6,則此三角形的周長為_________
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某股票市場,買、賣股票都要分別交納印花稅等有關稅費.以A市股的股票交易為例,除成本外還要交納:
①印花稅:按成交金額的0.1%計算;
②過戶費:按成交金額的0.1%計算;
③傭金:按不高于成交金額的0.3%計算(本題按0.3%計算),不足5元按5元計算,
例:某投資者以每股5.00元的價格在滬市A股中買入股票“金杯汽車”1000股,以每股5.50元的價格全部賣出,共盈利多少?
解:直接成本:5×1000=5000(元);
印花稅:(5000+5.50×1000)×0.1%=10.50(元);
過戶費:(5000+5.50×1000)×0.1%=10.50(元);
傭金:5000×0.3%=15.00(元) 5.50×1000×0.3%=16.50(元)
∵15.00>5 16.50>5 ∴傭金為15.00+16.50=31.50元.
總支出:5000+10.50+10.50+31.50=5052.50(元);
總收入:5.50×1000=5500(元);
總盈利:5500-5052.50=447.50(元).
問題:
(1)小王對此很感興趣,以每股5.00元的價格買入以上股票100股,以每股5.50元的價格全部賣出,則他盈利為______________元;
(2)小張以每股a(a≥5)元的價格買入以上股票1000股,股市波動大,他準備在不虧不盈時賣出.請你幫他計算出賣出的價格每股是多少元(用a的代數式表示)?
(3)小張再以每股5.00元的價格買入以上股票1000股,準備盈利1000元時才賣出,請你幫他計算賣出的價格每股是多少元?(精確到0.01元)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一條數軸在原點O和點B處各折一下,得到一條“折線數軸”.圖中點A表示﹣11,點B表示10,點C表示18,我們稱點A和點C在數軸上相距29個長度單位.動點P從點A出發,以2單位/秒的速度沿著“折線數軸”的正方向運動,從點O運動到點B期間速度變為原來的一半,之后立刻恢復原速;同時,動點Q從點C出發,以1單位/秒的速度沿著數軸的負方向運動,從點B運動到點O期間速度變為原來的兩倍,之后也立刻恢復原速.設運動的時間為t秒.

問:(1)動點P從點A運動至C點需要多少時間?
(2)P、Q兩點相遇時,求出相遇點M所對應的數是多少;
(3)求當t為何值時,P、O兩點在數軸上相距的長度與Q、B兩點在數軸上相距的長度相等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),將兩塊直角三角板的直角頂點C疊放在一起.
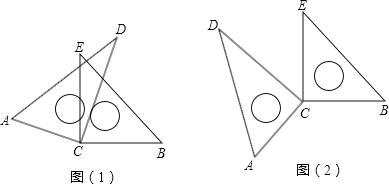
(1)試判斷∠ACE與∠BCD的大小關系,并說明理由;
(2)若∠DCE=30°,求∠ACB的度數;
(3)猜想∠ACB與∠DCE的數量關系,并說明理由;
(4)若改變其中一個三角板的位置,如圖(2),則第(3)小題的結論還成立嗎?(不需說明理由)
查看答案和解析>>
科目:初中數學 來源: 題型:
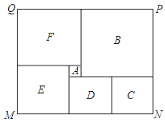
【題目】如圖的長方形MNPQ是州某市民健身廣場的平面示意圖,它是由6個正方形拼成的(分別用A,B,C,D,E,F六個字母表示).已知中間最小的正方形A的邊長是1米,設正方形C的邊長是x米.
(1)請用含x的代數式分別表示出正方形EF和B的邊長;
(2)觀察圖形的特點,找出兩個等量關系,分別用兩種方法列方程求出x的值;
(3)現沿著長方形廣場的四條邊鋪設下水管道,若甲,乙兩個工程隊單獨鋪設分別需要10天和15天完成,如果兩隊從M處開始,分別沿兩個不同方向同時施工![]() 天后,因甲隊另有任務,余下的工程由乙隊單獨施工10天完成,求
天后,因甲隊另有任務,余下的工程由乙隊單獨施工10天完成,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學對數據26,36,36,46,5■,52進行統計分析發現其中一個兩位數的個位數字被墨水涂污看不到了,則計算結果與被涂污數字無關的是( )
A.平均數B.中位數C.方差D.眾數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以線段AC為對角線的凸四邊形ABCD(它的四個頂點A、B、C、D按順時針方向排列,每個內角均小于180°),已知AB=BC=CD,∠ABC=120°,∠CAD=30°,則∠BCD的大小為____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com