
【題目】某校八年級舉行英語演講比賽,購買A,B兩種筆記本作為獎品,這兩種筆記本的單價分別是12元和8元.根據比賽設獎情況,需購買筆記本共30本,并且所購買A筆記本的數量要不多于B筆記本數量的![]() ,但又不少于B筆記本數量
,但又不少于B筆記本數量![]() ,設買A筆記本n本,買兩種筆記本的總費為w元.
,設買A筆記本n本,買兩種筆記本的總費為w元.
(1)寫出w(元)關于n(本)的函數關系式,并求出自變量n的取值范圍;
(2)購買這兩種筆記本各多少時,費用最少?最少的費用是多少元?
(3)商店為了促銷,決定僅對A種類型的筆記本每本讓利a元銷售,B種類型筆記本售價不變.問購買這兩種筆記本各多少本時花費最少?
【答案】(1)5≤n≤![]() ;(2)當n=5時,w取到最小值為260元;(3)當4﹣a>0,即a<4時,n=5,即買A筆記本5本,B筆記本25本,花費最少;當4﹣a=0,即a=4時,5≤n≤13,即買A筆記本5﹣13本,B筆記本25﹣17本,花費為240元;當4﹣a<0,即a>4時,n=13,即買A筆記本13本,B筆記本17本,花費最少.
;(2)當n=5時,w取到最小值為260元;(3)當4﹣a>0,即a<4時,n=5,即買A筆記本5本,B筆記本25本,花費最少;當4﹣a=0,即a=4時,5≤n≤13,即買A筆記本5﹣13本,B筆記本25﹣17本,花費為240元;當4﹣a<0,即a>4時,n=13,即買A筆記本13本,B筆記本17本,花費最少.
【解析】
(1)根據題意得到w(元)關于n(本)的函數關系式,可得到一個關于n的不等式組,可求出n的取值范圍,再結合花費的函數式,可求出x的具體數值;
(2)結合花費的函數式,可求出x的具體數值;
(3)根據a的取值范圍即可得到結論.
解:(1)由題意可知:w=12n+8(30﹣n),
∴w=4n+240,
又∵A筆記本的數量要不多于B筆記本數量的![]() ,但又不少于B筆記本數量的
,但又不少于B筆記本數量的![]() .
.
∴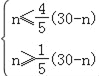 ,解得5≤n≤
,解得5≤n≤![]() ,
,
(2)w=4n+240,
∵k=4>0,
∴w隨n的增大而增大,
∴當n=5時,w取到最小值為260元.
(3)w=(12﹣a)n+8(30﹣n),
∴w=(4﹣a)n+240,
當4﹣a>0,即a<4時,n=5,即買A筆記本5本,B筆記本25本,花費最少,
當4﹣a=0,即a=4時,5≤n≤13,即買A筆記本5﹣13本,B筆記本25﹣17本,花費為240元,
當4﹣a<0,即a>4時,n=13,即買A筆記本13本,B筆記本17本,花費最少.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
【題目】問題背景:在△ABC中,AB、BC、AC三邊的長分別為![]() 、
、![]() 、
、![]() ,求此三角形的面積.小輝同學在解答這道題時,先建立一個正方形網格(每個小正方形的邊長為1),再在網格中畫出格點△ABC(即△ABC三個頂點都在小正方形的頂點處),如圖①所示.這樣不需求△ABC的高,而借用網格就能計算出它的面積.
,求此三角形的面積.小輝同學在解答這道題時,先建立一個正方形網格(每個小正方形的邊長為1),再在網格中畫出格點△ABC(即△ABC三個頂點都在小正方形的頂點處),如圖①所示.這樣不需求△ABC的高,而借用網格就能計算出它的面積.
(1)請你將△ABC的面積直接填寫在橫線上: .
思維拓展:
(2)我們把上述求△ABC面積的方法叫做構圖法.如果△ABC三邊的長分別![]() a、
a、![]() a、
a、![]() a(a>0),請利用圖②的正方形網格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.
a(a>0),請利用圖②的正方形網格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“永定樓”是門頭溝區的地標性建筑,某中學九年級數學興趣小組進行了測量它高度的社會實踐活動.如圖,他們在A點測得頂端D的仰角∠DAC=30°,向前走了46米到達B點后,在B點測得頂端D的仰角∠DBC=45°.求永定樓的高度CD.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年10月17日是我國第五個“扶貧日”,某校學生會干部對學生倡導的“扶貧”自愿捐款活動進行抽樣調查,得到一組學生捐款情況的數據,對學校部分捐款人數進行調查和分組統計后,將數據整理成如圖所示的統計圖,(圖中信息不完整),已知A.B兩組捐款人數的比為1:5.

被調查的捐款人數分組統計表:
組別 | 捐款額x/元 | 人數 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
請結合以上信息解答下列問題:
(1)求a的值和參與調查的總人數;
(2)補全“被調查的捐款人數分組統計圖1”并計算扇形B的圓心角度數;
(3)已知該校有學生2200人,請估計捐款數不少于30元的學生人數有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算題
(1)13×(﹣5)
(2)(﹣21)÷(﹣7)
(3)﹣3+(﹣5)﹣(﹣7)
(4)(﹣36![]() )÷9.
)÷9.
(5)11![]() ﹣(
﹣(![]() +2
+2![]() )
)
(6)![]() ÷1
÷1![]() ×3
×3![]() .
.
(7)(﹣0.5)+|0﹣6![]() |﹣(﹣7
|﹣(﹣7![]() )﹣(﹣4.75)
)﹣(﹣4.75)
(8)99![]() ×(﹣9)
×(﹣9)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,P、Q分別是BC、AC上的點,作PR⊥AB,PS⊥AC,垂足分別為R、S,若AQ=PQ,PR=PS,則結論:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正確的有( )

A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,D、E分別是AB、BC的中點,F在CA延長線上,∠FDA=∠B,AC=6,AB=8,則四邊形AEDF的周長為( )
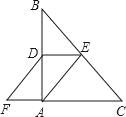
A. 16 B. 20 C. 18 D. 22
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段AD上一點,點B為CD的中點,且AD=8 cm,BD=2 cm.
(1)圖中共有多少條線段?
(2)求AC的長.
(3)若點E在直線AD上,且EA=3 cm,求BE的長.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1, 在 ![]() 中,
中, ![]() ,
, ![]() .點O是BC的中點,點D沿B→A→C方向從B運動到C.設點D經過的路徑長為
.點O是BC的中點,點D沿B→A→C方向從B運動到C.設點D經過的路徑長為 ![]() ,圖1中某條線段的長為y,若表示y與x的函數關系的圖象大致如圖2所示,則這條線段可能是圖1中的( )
,圖1中某條線段的長為y,若表示y與x的函數關系的圖象大致如圖2所示,則這條線段可能是圖1中的( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com