
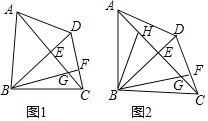
【題目】已知:在四邊形ABCD中,對角線AC、BD相交于點E,且AC⊥BD,作BF⊥CD,垂足為點F,BF與AC交于點C,∠BGE=∠ADE.
(1)如圖1,求證:AD=CD;
(2)如圖2,BH是△ABE的中線,若AE=2DE,DE=EG,在不添加任何輔助線的情況下,請直接寫出圖2中四個三角形,使寫出的每個三角形的面積都等于△ADE面積的2倍.
【答案】(1)證明見解析;(2)△ACD、△ABE、△BCE、△BHG.
【解析】(1)由AC⊥BD、BF⊥CD知∠ADE+∠DAE=∠CGF+∠GCF,根據∠BGE=∠ADE=∠CGF得出∠DAE=∠GCF即可得;
(2)設DE=a,先得出AE=2DE=2a、EG=DE=a、AH=HE=a、CE=AE=2a,據此知S△ADC=2a2=2S△ADE,證△ADE≌△BGE得BE=AE=2a,再分別求出S△ABE、S△ACE、S△BHG,從而得出答案.
(1)∵∠BGE=∠ADE,∠BGE=∠CGF,
∴∠ADE=∠CGF,
∵AC⊥BD、BF⊥CD,
∴∠ADE+∠DAE=∠CGF+∠GCF,
∴∠DAE=∠GCF,
∴AD=CD;
(2)設DE=a,
則AE=2DE=2a,EG=DE=a,
∴S△ADE=![]() AE×DE=
AE×DE=![]() ×2a×a=a2,
×2a×a=a2,
∵BH是△ABE的中線,
∴AH=HE=a,
∵AD=CD、AC⊥BD,
∴CE=AE=2a,
則S△ADC=![]() ACDE=
ACDE=![]() (2a+2a)a=2a2=2S△ADE;
(2a+2a)a=2a2=2S△ADE;
在△ADE和△BGE中,
∵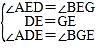 ,
,
∴△ADE≌△BGE(ASA),
∴BE=AE=2a,
∴S△ABE=![]() AEBE=
AEBE=![]() (2a)2a=2a2,
(2a)2a=2a2,
S△ACE=![]() CEBE=
CEBE=![]() (2a)2a=2a2,
(2a)2a=2a2,
S△BHG=![]() HGBE=
HGBE=![]() (a+a)2a=2a2,
(a+a)2a=2a2,
綜上,面積等于△ADE面積的2倍的三角形有△ACD、△ABE、△BCE、△BHG.


科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,AC是對角線,今有較大的直角三角板,一邊始終經過點B,直角頂點P在射線AC上移動,另一邊交DC于點Q.
(1)如圖①,當點Q在DC邊上時,猜想并寫出PB與PQ所滿足的數量關系,并加以證明;
(2)如圖②,當點Q落在DC的延長線上時,猜想并寫出PB與PQ滿足的數量關系,并證明你的猜想.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點B、F、C、E在一條直線上,AC=DF,BF=CE,那么添加下列一個條件后,仍無法判斷△ABC≌△DEF的是( )
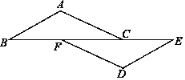
A. ∠A=∠D=90° B. ∠BCA=∠EFD C. ∠B=∠E D. AB=DE
查看答案和解析>>
科目:初中數學 來源: 題型:
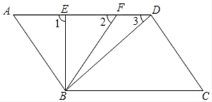
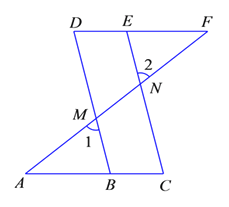
【題目】如圖,已知AD∥BC,∠A=∠C=50°,線段AD上從左到右依次有兩點E、F(不與A、D重合)
(1)AB與CD是什么位置關系,并說明理由;
(2)觀察比較∠1、∠2、∠3的大小,并說明你的結論的正確性;
(3)若∠FBD:∠CBD=1:4,BE平分∠ABF,且∠1=∠BDC,求∠FBD的度數,判斷BE與AD是何種位置關系?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】結合圖形填空:已知:如圖![]() ,
,![]() .求證:
.求證:![]() .
.
證明:∵![]() (已知),
(已知),
又![]() ( ),
( ),
∴![]() (等量代換),
(等量代換),
∴![]() (同位角相等,兩直線平行),
(同位角相等,兩直線平行),
∴![]() ( ).
( ).
∵![]() (已知),
(已知),
∴![]() (等量代換),
(等量代換),
∴![]() ( ),
( ),
∴![]() ( ).
( ).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形MNOK和正六邊形ABCDEF邊長均為1,把正方形放在正六邊形中,使OK邊與AB邊重合,如圖所示,按下列步驟操作: 將正方形在正六邊形中繞點B順時針旋轉,使KM邊與BC邊重合,完成第一次旋轉;再繞點C順時針旋轉,使MN邊與CD邊重合,完成第二次旋轉;…在這樣連續6次旋轉的過程中,點B,M間的距離可能是( )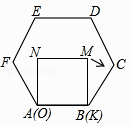
A.1.4
B.1.1
C.0.8
D.0.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com