
【題目】課題研究
(1)閱讀下面材料:
如圖所示,點A、B在數軸上分別表示有理數a,b,A、B兩點之間的距離表示為![]() .當A、B兩點中有一點在原點時,不妨設點A在原點,如圖甲所示,
.當A、B兩點中有一點在原點時,不妨設點A在原點,如圖甲所示,![]() ;當A、B兩點都不在原點時:
;當A、B兩點都不在原點時:
①如圖乙所示,點A、B都在原點的右邊,![]()
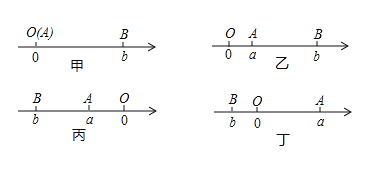
②如圖丙所示,點A、B都在原點的左邊,![]()
③如圖丁所示,點A、B在原點的兩邊,![]()
綜上,數軸上A、B兩點之間的距離為![]() =______________________.
=______________________.
(2)回答下列問題:
①數軸上表示2和5的兩點之間的距離是_______
②數軸上表示-2和-5的兩點之間的距離是_______
③數軸上表示1和-3的兩點之間的距離是_______
④數軸上表示x和-1的兩點之間的距離是_______
⑤如果![]() =2,那么x的值為______________
=2,那么x的值為______________
科目:初中數學 來源: 題型:
【題目】 某校為了解九年級男同學的體育考試準備情況,隨機抽取部分男同學進行了1000米跑測試.按照成績分為優秀、良好、合格與不合格四個等級.學校繪制了如下不完整的統計圖.
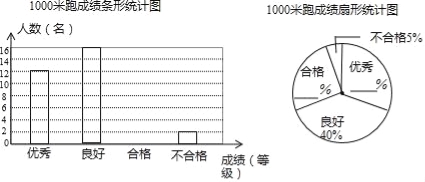
(1)根據給出的信息,補全兩幅統計圖;
(2)該校九年級有600名男生,請估計成績未達到良好有多少名?
(3)某班甲、乙兩位成績優秀的同學被選中參加即將舉行的學校運動會1000米比賽,預賽分為A、B、C三組進行,選手由抽簽確定分組.甲、乙兩人恰好分在同一組的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小剛和小強從![]() 兩地同時出發,小剛騎自行車,小強步行,沿同一條路線相向勻速而行.出發后兩小時兩人相遇,相遇時小剛比小強多行進24千米.相遇后0.5小時小剛到達
兩地同時出發,小剛騎自行車,小強步行,沿同一條路線相向勻速而行.出發后兩小時兩人相遇,相遇時小剛比小強多行進24千米.相遇后0.5小時小剛到達![]() 地.
地.
(1)兩人的行進速度分別是多少?
(2)相遇后經過多少時間小強到達![]() 地?
地?
(3)![]() 兩地相距多少千米?
兩地相距多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是本地區一種產品30天的銷售圖象,圖1是產品日銷售量y(單位:件)與時間t(單位:天)的函數關系,圖2是一件產品的銷售利潤z(單位:元)與時間t(單位:天)的函數關系,已知日銷售利潤=日銷售量×一件產品的銷售利潤,下列結論錯誤的是( )

A. 第24天的銷售量為200件 B. 第10天銷售一件產品的利潤是15元
C. 第12天與第30天這兩天的日銷售利潤相等 D. 第30天的日銷售利潤是750元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,已知點![]() 在線段
在線段![]() 上,且
上,且![]() ,
,![]() ,點
,點![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,求線段
的中點,求線段![]() 的長度;
的長度;
![]()
(2)若點![]() 是線段
是線段![]() 上任意一點,且
上任意一點,且![]() ,
,![]() ,點
,點![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,請直接寫出線段
的中點,請直接寫出線段![]() 的長度;(結果用含
的長度;(結果用含![]() 、
、![]() 的代數式表示)
的代數式表示)
(3)在(2)中,把點![]() 是線段
是線段![]() 上任意一點改為:點
上任意一點改為:點![]() 是直線
是直線![]() 上任意一點,其他條件不變,則線段
上任意一點,其他條件不變,則線段![]() 的長度會變化嗎?若有變化,求出結果.
的長度會變化嗎?若有變化,求出結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展“唱紅歌”比賽活動,九年級(1)、(2)班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績如圖所示.
班級 | 平均數(分) | 中位數 | 眾數 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根據圖示填寫上表;
(2)結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
(3)計算兩班復賽成績的方差,并說明哪個班級的成績較穩定.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形紙片ABCD中,AB=3cm,AD=5cm,折疊紙片使B點落在邊AD上的E處,折痕為PQ,過點E作EF∥AB交PQ于F,連接BF.
(1)求證:四邊形BFEP為菱形;
(2)當點E在AD邊上移動時,折痕的端點P、Q也隨之移動;
①當點Q與點C重合時(如圖2),求菱形BFEP的邊長;
②若限定P、Q分別在邊BA、BC上移動,求出點E在邊AD上移動的最大距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圖形中每一小格正方形的邊長為1,已知△ABC
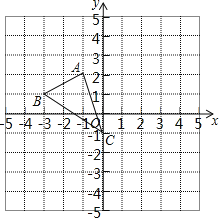
(1)AC的長等于 .(結果保留根號)
(2)將△ABC向右平移2個單位得到△A′B′C′,則A點的對應點A′的坐標是 ;
(3)畫出將△ABC繞點C按順時針方向旋轉90°后得到△A1B1C1,并寫出A點對應點A1的坐標?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據材料,解答問題
如圖,數軸上有點![]() ,對應的數分別是6,-4,4,-1,則
,對應的數分別是6,-4,4,-1,則![]() 兩點間的距離為
兩點間的距離為![]() ;
;![]() 兩點間的距離為
兩點間的距離為![]() ;
;![]() 兩點間的距離為
兩點間的距離為![]() ;由此,若數軸上任意兩點
;由此,若數軸上任意兩點![]() 分別表示的數是
分別表示的數是![]() ,則
,則![]() 兩點間的距離可表示為
兩點間的距離可表示為![]() .反之,
.反之,![]() 表示有理數
表示有理數![]() 在數軸上的對應點
在數軸上的對應點![]() 之間的距離,稱之為絕對值的幾何意義.
之間的距離,稱之為絕對值的幾何意義.
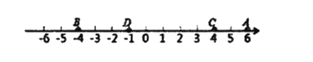
問題應用1:
(1)如果表示-1的點![]() 和表示
和表示![]() 的點
的點![]() 之間的距離是2,則點
之間的距離是2,則點![]() 對應的
對應的![]() 的值為___________;
的值為___________;
(2)方程![]() 的解
的解![]() ____________;
____________;
(3)方程![]() 的解
的解![]() ______________ ;
______________ ;
問題應用2:
如圖,若數軸上表示![]() 的點為
的點為![]() .
.
(4)![]() 的幾何意義是數軸上_____________,當
的幾何意義是數軸上_____________,當![]() __________,
__________,![]() 的值最小是____________;
的值最小是____________;
(5)![]() 的幾何意義是數軸上_______,
的幾何意義是數軸上_______,![]() 的最小值是__________,此時點
的最小值是__________,此時點![]() 在數軸上應位于__________上;
在數軸上應位于__________上;
(6)根據以上推理方法可求![]() 的最小值是___________,此時
的最小值是___________,此時![]() __________.
__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com