【題目】某市計劃在城區投放一批“共享單車”，這批單車分為A，B兩種不同款型，其中A型車單價400元，B型車單價320元．
（1）在“共享單車”試點，投放A，B兩種款型的單車共100輛，總價值36 800元．試問本次試點投放的A型車與B型車各多少輛？
設本次試點投放的A型車
輛、B型車
輛．
根據題意，列方程組___________
解這個方程組，得___________
答： ．
（2）該市決定在整個城區投放 “共享單車”．按照（Ⅰ）中試點投放A，B兩車型的數量比進行投放，且投資總價值不低于184萬元．請問整個城區投放的A型車至少多少輛？
【答案】（1）
，
，A型車60輛B型車40輛；（2）A型車至少3000輛
【解析】
（1）設本次試點投放的A型車
輛、B型車
輛．依據“總價值36 800元”列出方程組，解之可得；
（2）由（1）知A、B型車輛的數量比是3:2，故可設A型車3a輛，B型車2a輛，根據“投資總價值不低于184萬元”列出關于a的不等式，解之求得a的取值范圍，進一步求解可得.
（1） 設本次試點投放的A型車輛、B型車輛．
根據題意，列方程組
解這個方程組，得
答：A型車60輛B型車40輛
（2）由（1）知A、B型車輛的數量比是3:2，故設A型車3a輛 B型車2a輛，根據題意，得：
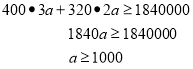
答：整個城區投放的A型車至少3000輛.
科目：初中數學 來源： 題型：
【題目】甲、乙兩支儀仗隊各10名隊員的身高（單位：cm）如下表：
甲隊 | 179 | 177 | 178 | 177 | 178 | 178 | 179 | 179 | 177 | 178 |
乙隊 | 178 | 178 | 176 | 180 | 180 | 178 | 176 | 179 | 177 | 178 |
（1）甲隊隊員的平均身高為cm，乙隊隊員的平均身高為cm；
（2）請用你學過的統計知識判斷哪支儀仗隊的身高更為整齊呢？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線 
（1）該拋物線的對稱軸是 ， 頂點坐標；
（2）選取適當的數據填入下表，并在直角坐標系內描點畫出該拋物線的圖象；
x | … | … | |||||
y | … | … |
（3）若該拋物線上兩點A（x1 ， y1），B（x2 ， y2）的橫坐標滿足x1＞x2＞1，試比較y1與y2的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示,請按照要求解答問題.
(1)數軸上的點C在2、3的正中間位置,則點C表示的數是 ,線段AB的中點D表示的數是 ;
(2)線段AB的中點D與線段BC的中點E的距離為 ;
(3)在數軸上方有一點M,下方有一點N,且∠ABM=120°,∠CBN=60°,請畫出示意圖,并判斷BC是否平分∠MBN.簡要說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是正方形，其中A（
，
），B（
，），C（，
），將這個正方形向左平移3個單位長度，再向上平移1個單位長度，得正方形
．
（1）畫出平移后的正方形；
（2）寫出點D和點D′ 的坐標；
（3）寫出線段
與
的位置和大小關系．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若關于x的一元二次方程（x-2）（x-3）=m有實數根x1 ， x2 ， 且x1
x2有下列結論：①x1=2,x2=3；②m> 
；③二次函數y=（x-x1）（x-x2）+m的圖象與x軸交點的坐標為（2,0）和（3,0）.其中正確的結論是（填正確結論的序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線AB∥CD，直線EF分別與AB、CD交于點M、N，點H在直線CD上，HG⊥EF于點G，過點G作GP∥AB．則下列結論：①∠AMF與∠DNF是對頂角；②∠PGM＝∠DNF；③∠BMN+∠GHN＝90°；④∠AMG+∠CHG＝270°．其中正確結論的個數（ ）
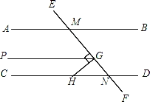
A.1個B.2 個C.3個D.4個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（探究活動）
（1）問題發現：如圖①，直線AB∥CD，E是AB與AD之間的一點，連接BE，CE，可以發現∠B+∠C=∠BEC．
請把下面的證明過程補充完整：
證明：過點E作EF∥AB，
∵AB∥DC（已知），EF∥AB（輔助線的作法），
∴EF∥DC（ ）
∴∠C=∠CEF．（ ）
∵EF∥AB，∴∠B=∠BEF（同理），
∴∠B+∠C= （等量代換）
即∠B+∠C=∠BEC．
（2）拓展探究：如果點E運動到圖②所示的位置，其他條件不變，試探究∠B、∠C、∠BEC的數量關系并證明；
（3）解決問題：如圖③，AB∥DC，∠C=120°，∠AEC=80°，則∠A= ．（直接寫出結論，不用寫計算過程）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ABC=90°，BC=6，D為AC延長線上一點，AC=3CD，過點D作DH∥AB，交BC的延長線于點H．
（1）求BH的長；
（2）若AB=12，試判斷∠CBD與∠A的數量關系，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com