
【題目】直線DE上有一點O,過點O在直線DE上方作射線OC,將直角三角板AOB(∠OAB=30°)的直角頂點放在點O處,一條直角邊OA在射線OD上,另一邊OB在直線DE上方.將直角三角板繞點O按每秒10°的速度逆時針旋轉得到三角形A'OB',三角形AOB旋轉一周后停止旋轉,設旋轉時間為t秒.若射線OC的位置保持不變,∠COD=40°.
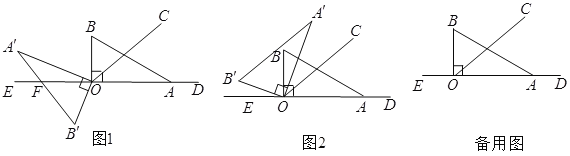
(1)如圖1,在旋轉過程中,當邊A'B'與直線DE相交于點F時,請用含t的代數式分別表示∠A'OC和∠B'OF的度數,并求出∠A'OC-∠B'OF的值;
(2)如圖2,當t=7時,試說明直線A'B'//OC;
(3)在旋轉過程中,若t=7,是否還存在某一時刻,使得A'B'//OC;若存在,請求出符合條件的t值;若不存在,請說明理由.
【答案】∠A′OC=10°t-40°,∠B′OF=10°t-90°,50°;(2)詳見解析;(3)t=25.
【解析】
(1)根據∠A′OC=∠A′OD-∠COD,∠B′OF=∠B'OB-∠BOF用含t的式子表示出∠A'OC,∠B′OF,然后計算∠A'OC﹣∠B′OF即可;
(2)把t=7代入∠A′OC的表達式,求出∠A′OC的度數,得到∠A′OC=∠A′,根據內錯角相等,兩直線平行即可得到結論;
(3)根據同旁內角互補,兩直線平行,當∠A′OC+∠A′=180°時,A′B′∥OC,列方程得:360°-(10°t-40°)+30°=180°,求解即可.
(1)∠A′OC=∠A′OD-∠COD=10°t-40°,∠B′OF=∠B'OB-∠BOF=10°t-90°,
∠A'OC﹣∠B′OF=(10°t-40°)-(10°t-90°)=50°.
(2)因為t=7,所以∠A′OC=10°×7-40°=30°,
因為∠A′=∠A=30°,
所以∠A′OC=∠A′,
所以A′B′∥OC;(內錯角相等,兩直線平行)
(3)如圖,
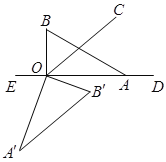
當∠A′OC+∠A′=180°時,
A′B′∥OC,(同旁內角互補,兩直線平行)
所以360°-(10°t-40°)+30°=180°,
解得:t=25.


 寒假學與練系列答案
寒假學與練系列答案科目:初中數學 來源: 題型:
【題目】建設中的大外環路是我市的一項重點民生工程.某工程公司承建的一段路基工程的施工土方量為120萬立方,原計劃由公司的甲、乙兩個工程隊從公路的兩端同時相向施工150天完成.由于特殊情況需要,公司抽調甲隊外援施工,由乙隊先單獨施工40天后甲隊返回,兩隊又共同施工了110天,這時甲乙兩隊共完成土方量103.2萬立方.
(1)問甲、乙兩隊原計劃平均每天的施工土方量分別為多少萬立方?
(2)在抽調甲隊外援施工的情況下,為了保證150天完成任務,公司為乙隊新購進了一批機械來提高效率,那么乙隊平均每天的施工土方量至少要比原來提高多少萬立方才能保證按時完成任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
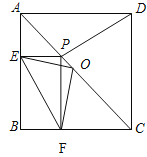
【題目】如圖,已知:在正方形ABCD中,點P在AC上,PE⊥AB于E,PF⊥BC于F.
(1)試判斷線段EF與PD的長是否相等,并說明理由.
(2)若點O是AC的中點,判斷OF與OE之間有怎樣的位置和數量關系?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】多項式4x2+1加上一個單項式,使它成為一個整式的完全平方,則這個單項式可以是__________________.(填寫符合條件的一個即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場第1次用39萬元購進A、B兩種商品,銷售完后獲得利潤6萬元,它們的進價和售價如下表:(總利潤=單件利潤×銷售量)
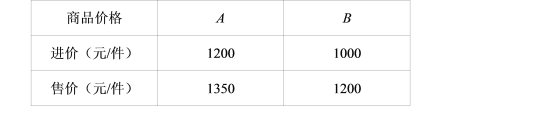
(1)該商場第1次購進A、B兩種商品各多少件?
(2)商場第2次以原價購進A、B兩種商品,購進A商品的件數不變,而購進B商品的件數是第1次的2倍,A商品按原價銷售,而B商品打折銷售,若兩種商品銷售完畢,要使得第2次經營活動獲得利潤等于54000元,則B種商品是打幾折銷售的?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一組有規律的圖案,它們是由邊長相同的正方形和正三角形拼接而成,第①個圖案有4個三角形和1個正方形,第②個圖案有7個三角形和2個正方形,第③個圖案有10個三角形和3個正方形,…依此規律,第n個圖案有 ____________個三角形(用含n的代數式表示);

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為積極響應“弘揚傳統文化”的號召,某學校倡導全校1200名學生進行經典詩詞誦背活動,并在活動之后舉辦經典詩詞大賽,為了解本次系列活動的持續效果,學校團委在活動啟動之初,隨機抽取部分學生調查“一周詩詞誦背數量”,根調查結果繪制成的統計圖(部分)如圖所示.
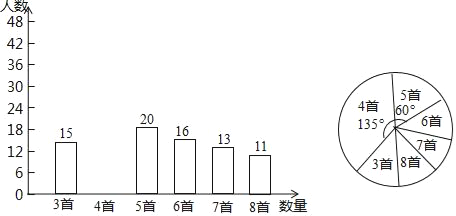
大賽結束后一個月,再次抽查這部分學生“一周詩詞誦背數量”,繪制成統計表
一周詩詞誦背數量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人數 | 10 | 10 | 15 | 40 | 25 | 20 |
請根據調查的信息
(1)活動啟動之初學生“一周詩詞誦背數量”的中位數為 ;
(2)估計大賽后一個月該校學生一周詩詞誦背6首(含6首)以上的人數;
(3)選擇適當的統計量,從兩個不同的角度分析兩次調查的相關數據,評價該校經典詩詞誦背系列活動的效果.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com