
【題目】已知數列{an} 滿足a1= ![]() ,a2=
,a2= ![]() ,an+2﹣an+1=(﹣1)n+1(an+1﹣an)(n∈N*),數列{an}的前n項和為Sn , 則S2017= .
,an+2﹣an+1=(﹣1)n+1(an+1﹣an)(n∈N*),數列{an}的前n項和為Sn , 則S2017= .
【答案】![]()
【解析】解:數列{an} 滿足a1= ![]() ,a2=
,a2= ![]() ,an+2﹣an+1=(﹣1)n+1(an+1﹣an)(n∈N*), ∴n=2k(k∈N*)時,a2k+2﹣a2k+1=﹣a2k+1+a2k , 即a2k+2=a2k=
,an+2﹣an+1=(﹣1)n+1(an+1﹣an)(n∈N*), ∴n=2k(k∈N*)時,a2k+2﹣a2k+1=﹣a2k+1+a2k , 即a2k+2=a2k= ![]() .
.
n=2k﹣1(k∈N*)時,a2k+1﹣a2k=a2k﹣a2k﹣1 , 可得a2k+1+a2k﹣1=2a2k= ![]() .
.
∴S2017=a1+(a3+a5)+…+(a2015+a2017)+a2+a4+…+a2016
= ![]() +
+ ![]() ×504+
×504+ ![]()
= ![]() .
.
所以答案是: ![]() .
.
【考點精析】利用數列的前n項和對題目進行判斷即可得到答案,需要熟知數列{an}的前n項和sn與通項an的關系 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】現有四個函數:①y=xsinx;②y=xcosx;③y=x|cosx|;④y=x2x的圖象(部分)如圖: 
則按照從左到右圖象對應的函數序號安排正確的一組是( )
A.①④③②
B.③④②①
C.④①②③
D.①④②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,直四棱柱ABCD﹣A1B1C1D1內接于半徑為 ![]() 的半球O,四邊形ABCD為正方形,則該四棱柱的體積最大時,AB的長是( )
的半球O,四邊形ABCD為正方形,則該四棱柱的體積最大時,AB的長是( ) 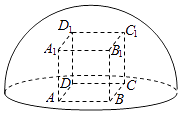
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數 ![]() . (Ⅰ)求函數f(x)的單調遞增區間;
. (Ⅰ)求函數f(x)的單調遞增區間;
(Ⅱ)在△ABC中,內角A、B、C的對邊分別為a、b、c.已知 ![]() ,a=2,
,a=2, ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代內容極為豐富的數學名著,書中有如下問題:“今有五人五錢,令上二人所得與下三人等.問各得幾何?”其意思為:“現有甲乙丙丁戊五人依次差值等額分五錢,要使甲乙兩人所得的錢與丙丁戊三人所得的錢相等,問每人各得多少錢?”根據題意,乙得( )
A.![]() 錢
錢
B.![]() 錢
錢
C.1錢
D.![]() 錢
錢
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】函數f(x)= ![]() +a(x﹣1)﹣2.
+a(x﹣1)﹣2.
(1)當a=0時,求函數f(x)的極值;
(2)若對任意x∈(0,1)∪(1,+∞),不等式 ![]() <
< ![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校學生利用雙休時間去距學校10km的炎帝故里參觀,一部分學生騎自行車先走,過了20min后,其余學生乘汽車沿相同路線出發,結果他們同時到達.已知汽車的速度是騎車學生速度的2倍,求騎車學生的速度和汽車的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售A,B兩種品牌的教學設備,這兩種教學設備的進價和售價如表所示
A | B | |
進價(萬元/套) | 1.5 | 1.2 |
售價(萬元/套) | 1.65 | 1.4 |
該商場計劃購進兩種教學設備若干套,共需66萬元,全部銷售后可獲毛利潤9萬元.
(1)該商場計劃購進A,B兩種品牌的教學設備各多少套?
(2)通過市場調研,該商場決定在原計劃的基礎上,減少A種設備的購進數量,增加B種設備的購進數量,已知B種設備增加的數量是A種設備減少的數量的1.5倍.若用于購進這兩種教學設備的總資金不超過69萬元,問A種設備購進數量至多減少多少套?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某旅游風景區出售一種紀念品,該紀念品的成本為12元/個,這種紀念品的銷售價格為x(元/個)與每天的銷售數量y(個)之間的函數關系如圖所示. 
(1)求y與x之間的函數關系式;
(2)銷售價格定為多少時,每天可以獲得最大利潤?并求出最大利潤.
(3)“十一”期間,游客數量大幅增加,若按八折促銷該紀念品,預計每天的銷售數量可增加200%,為獲得最大利潤,“十一”假期該紀念品打八折后售價為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com