【題目】如圖，在矩形ABCD中，AB=5，BC=10 
，一圓弧過點B和點C，且與AD相切，則圖中陰影部分面積為 ． 
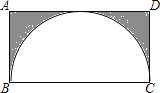
【答案】75 
﹣ 
【解析】解：設圓弧的圓心為O，與AD切于E，
連接OE交BC于F，連接OB、OC，
設圓的半徑為x，則OF=x﹣5，
由勾股定理得，OB2=OF2+BF2 ，
即x2=（x﹣5）2+（5 ）2 ，
解得，x=5，
則∠BOF=60°，∠BOC=120°，
則陰影部分面積為：矩形ABCD的面積﹣（扇形BOCE的面積﹣△BOC的面積）
=10 ×5﹣ 
+ 
×10 ×5=75 ﹣ ，
所以答案是：75 ﹣ ．
【考點精析】本題主要考查了矩形的性質和切線的性質定理的相關知識點，需要掌握矩形的四個角都是直角，矩形的對角線相等；切線的性質：1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑才能正確解答此題．
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知拋物線y=x2+bx+c過A，B，C三點，點A的坐標是（3，0），點C的坐標是（0，﹣3），動點P在拋物線上．
（1）b= ， c= ， 點B的坐標為；（直接填寫結果）
（2）是否存在點P，使得△ACP是以AC為直角邊的直角三角形？若存在，求出所有符合條件的點P的坐標；若不存在，說明理由；
（3）過動點P作PE垂直y軸于點E，交直線AC于點D，過點D作x軸的垂線．垂足為F，連接EF，當線段EF的長度最短時，求出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，向一個半徑為R、容積為V的球形容器內注水，則能夠反映容器內水的體積y與容器內水深x間的函數關系的圖象可能是（ ）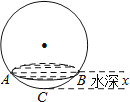 
A.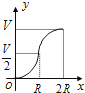
B.
C.
D.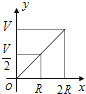
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點A，B的坐標分別為（－1，0），（3，0），現同時將點A，B分別向上平移2個單位，再向右平移1個單位，分別得到點A，B的對應點C，D，連接AC，BD，CD．
（1）求點C，D的坐標及平行四邊形ABDC的面積
.
（2）在y軸上是否存在一點P，連接PA，PB，使
＝2，若存在這樣一點，求出點P的坐標，若不存在，試說明理由．
（3）點P是四邊形ABCD邊上的點，若△OPC為等腰三角形時，直接寫出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】以下列數組作為三角形的三條邊長，其中能構成直角三角形的是( )
A. 1， 
，3 B. 
， 
，5 C. 1.5，2，2.5 D. 
， 
， 
【答案】C
【解析】A、12+（
）2≠32，不能構成直角三角形，故選項錯誤；
B、(
2+（
）2≠52，不能構成直角三角形，故選項錯誤；
C、1.52+22=2.52，能構成直角三角形，故選項正確；
D、（
））2+（
）2≠（
）2，不能構成直角三角形，故選項錯誤．
故選：C．
【題型】單選題
【結束】
3
【題目】在Rt△ABC中，∠C=90°，AC=9，BC=12，則點C到斜邊AB的距離是（ ）
（A）
（B）
（C）9 （D）6
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖1，已知△ABC，以AB、AC為邊分別向外作正方形ABFD和正方形ACGE，連結BE、CD，猜想BE與CD有什么數量關系？并說明理由；
（2）請模仿正方形情景下構造全等三角形的思路，利用構造全等三角形完成下題：如圖2，要測量池塘兩岸相對的兩點B、E的距離，已經測得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的長（結果保留根號）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，G是BD上一點，連接CG并延長交BA的延長線于點F，交AD于點E．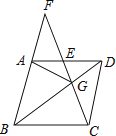
（1）求證：AG=CG．
（2）求證：AG2=GEGF．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在如圖所示的網格中，線段AB和直線a如圖所示，方格紙中每個小正方形的邊長均為1，線段AB的兩個端點均在格點上．
（1）在圖中畫出以線段AB為一邊的正方形 ABCD，且點C和點D均在格點上，
并直接寫出正方形 ABCD的面積為 ；
（2）在圖中以線段AB為一腰的等腰三角形ABE，點E在格點上，則滿足條件的點E有_____ 個；
（3）在圖中的直線a上找一點Q，使得△QAB的周長最小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
