
【題目】小明是一位善于思考的學生,在一次數學活動課上,他將一副直角三角板按如圖所示的位置擺放,A、B、D三點在同一直線上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8. 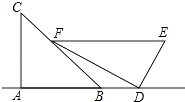
(1)試求點F到AD的距離.
(2)試求BD的長.
【答案】
(1)解:如圖,過點F作FM⊥AD于點M,
在△EDF中,∠EDF=90°,∠E=60°,DE=8,
則∠DFE=30°,
故EF=2DE=16,
DF= ![]() =
= ![]() =8
=8 ![]() ,
,
∵AB∥EF,
∴∠FDM=∠DFE=30°,
在Rt△FMD中,MF= ![]() DF=8
DF=8 ![]() ×
× ![]() =4
=4 ![]() ,
,
即點F與AD之間的距離為:4 ![]()
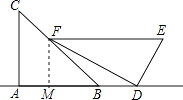
(2)解:在Rt△FMD中,DM= ![]() =
= ![]() =12,
=12,
∵∠C=45°,∠CAB=90°,
∴∠CBA=45°,
又∵∠FMB=90°,
△FMB是等腰直角三角形,
∴MB=FM=4 ![]() ,
,
∴BD=MD﹣FM=12﹣4 ![]()
【解析】(1)根據題意得出∠DFE=30°,則EF=2DE=16,進而利用勾股定理得出DF的長,進而得出答案;(2)直接利用勾股定理得出DM的長,進而得出MB=FM,求出答案.
【考點精析】根據題目的已知條件,利用平行線的性質和勾股定理的概念的相關知識可以得到問題的答案,需要掌握兩直線平行,同位角相等;兩直線平行,內錯角相等;兩直線平行,同旁內角互補;直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2.


科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,點D是BC上一點,∠BAD=80°,AB=AD=DC,則∠C的大小為( ) 
A.50°
B.40°
C.20°
D.25°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學表達式:(1)﹣3<0(2)3x+5>0(3)x2﹣6(4)x=﹣2(5)y≠0(6)x≥50中,不等式的個數是()
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC與BD相交于點O,MN過點O且與邊AD、BC分別交于點M和點N. 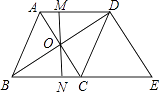
(1)請你判斷OM和ON的數量關系,并說明理由;
(2)過點D作DE∥AC交BC的延長線于點E,當AB=6,AC=8時,求△BDE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線a、b被直線c所截,下列說法正確的是( ) 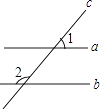
A.當∠1=∠2時,一定有a∥b
B.當a∥b時,一定有∠1=∠2
C.當a∥b時,一定有∠1+∠2=90°
D.當∠1+∠2=180°時,一定有a∥b
查看答案和解析>>
科目:初中數學 來源: 題型:
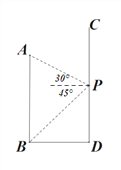
【題目】如圖,AB、CD分別表示兩幢相距36米的大樓,小明同學站在CD大樓的P處窗口觀察AB大樓的底部B點的俯角為45°,觀察AB大樓的頂部A點的仰角為30°.
(1)求PD的高;
(2)求大樓AB的高.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com