
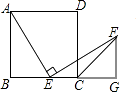
【題目】如圖,在正方形ABCD中,點E(與點B、C不重合)是BC邊上一點,將線段EA繞點E順時針旋轉90°到EF,過點F作BC的垂線交BC的延長線于點G,連接CF. 
(1)求證:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF , 求BE.
【答案】
(1)證明:∵EP⊥AE,
∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°,
∴∠GEF=∠BAE,
又∵FG⊥BC,
∴∠ABE=∠EGF=90°,
在△ABE與△EGF中,
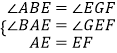 ,
,
∴△ABE≌△EGF(AAS)
(2)解:∵△ABE≌△EGF,AB=2,
∴AB=EG=2,S△ABE=S△EGF,
∵S△ABE=2S△ECF,
∴SEGF=2S△ECF,
∴EC=CG=1,
∵四邊形ABCD是正方形,
∵BC=AB=2,
∴BE=2﹣1=1.
【解析】(1)根據同角的余角相等得到一對角相等,再由一對直角相等,且AE=EF,利用AAS得到三角形ABE與三角形EFG全等;(2)利用全等三角形的性質得出AB=EG=2,S△ABE=S△EGF , 求出SEGF=2S△ECF , 根據三角形面積得出EC=CG=1,根據正方形的性質得出BC=AB=2,即可求出答案.此題屬于四邊形綜合題,涉及的知識有:全等三角形的判定與性質,正方形的性質,三角形的面積,熟練掌握判定與性質是解本題的關鍵.


 高中必刷題系列答案
高中必刷題系列答案科目:初中數學 來源: 題型:
【題目】星期六早晨蕊蕊媽媽從家里出發去觀山湖公園鍛煉,她連續、勻速走了60min后回家,圖中的折線段OA﹣AB﹣BC是她出發后所在位置離家的距離s(km)與行走時間t(min)之間的函數關系,則下列圖形中可以大致描述蕊蕊媽媽行走的路線是( ) 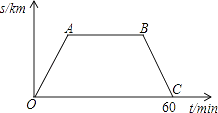
A.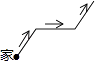
B.
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線L:y=ax2+bx+c與x軸交于A、B(3,0)兩點(A在B的左側),與y軸交于點C(0,3),已知對稱軸x=1.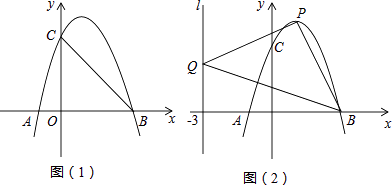
(1)求拋物線L的解析式;
(2)將拋物線L向下平移h個單位長度,使平移后所得拋物線的頂點落在△OBC內(包括△OBC的邊界),求h的取值范圍;
(3)設點P是拋物線L上任一點,點Q在直線l:x=﹣3上,△PBQ能否成為以點P為直角頂點的等腰直角三角形?若能,求出符合條件的點P的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】葛藤是一種刁鉆的植物,它自己腰桿不硬,為了爭奪雨露陽光,常常饒著樹干盤旋而上,它還有一手絕招,就是它繞樹盤上升的路線,總是沿著最短路線——盤旋前進的。難道植物也懂得數學嗎?
閱讀以上信息,你能設計一種方法解決下列問題嗎?
(1)如圖,如果樹的周長為3cm,從點A繞一圈到B點,葛藤升高4cm,則它爬行路程是多少厘米?
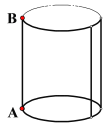
(2)如果樹的周長為8cm,繞一圈爬行10cm,則爬行一圈升高多少厘米?如果爬行10圈到達樹頂,則樹干高多少厘米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,對于一個圖形,通過兩種不同的方法計算它的面積,可以得到一個等式.例
如圖1可以得到![]() .請解答下列問題:
.請解答下列問題:

(1)根據圖2,完成數學等式: ![]() = ;
= ;
(2)觀察圖3,寫出圖3中所表示的等式: =____________.
(3)若![]() 、
、![]() 、
、![]() ,且
,且![]() ,請利用(2)所得的結論求:
,請利用(2)所得的結論求:![]() 的值
的值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com