
【題目】某校為了解初中學生每天在校體育活動的時間(單位:h),隨機調査了該校的部分初中學生.根據調查結果,繪制出如下的統計圖1和圖2.請根據相關信息,解答下列問題:
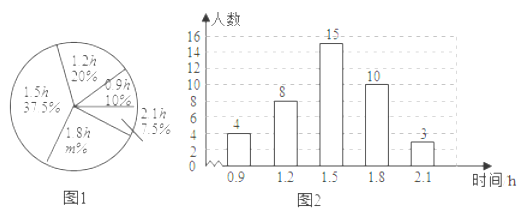
(Ⅰ)本次接受調查的初中學生人數為 ,圖1中m的值為 ;
(Ⅱ)求統計的這組每天在校體育活動時間數據的眾數和中位數;
(Ⅲ)根據統計的這組每天在校體育活動時間的樣本數據,若該校共有1200名初中學生,估計該校每天在校體育活動時間大于1h的學生人數.
【答案】(Ⅰ)40,25;(Ⅱ)眾數是1.5,中位數是1.5;(Ⅲ)1080人
【解析】
(Ⅰ)根據統計圖中的數據可以求得本次調查的學生人數,進而求得m的值;
(Ⅱ)根據統計圖中的數據可以求得這組數據的平均數和眾數、中位數;
(Ⅲ)根據統計圖中的數據可以求得該校每天在校體育活動時間大于1h的學生人數.
(Ⅰ)本次接受調查的初中學生人數為:4÷10%=40,
m%=![]() =25%,
=25%,
故答案為:40,25.
(Ⅱ)由條形統計圖得,4個0.9,8個1.2,15個1.5,10個1.8,3個2.1,
∴1.5出現的次數最多,15次,
∴眾數是1.5,
第20個數和第21個數都是1.5,
∴中位數是1.5;
(Ⅲ)1200×![]() =1080(人),
=1080(人),
答:該校每天在校體育活動時間大于1h的學生有1080人.


科目:初中數學 來源: 題型:
【題目】某中學舉行鋼筆書法大賽,對各年級同學的獲獎情況進行了統計,并繪制了如下兩幅不完整的統計圖.
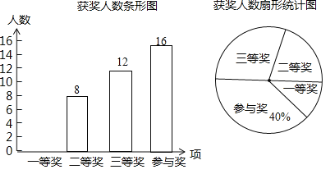
請結合圖中相關信息解答下列問題:
(1)扇形統計圖中三等獎所在扇形的圓心角的度數是______度;
(2)請將條形統計圖補全;
(3)獲得一等獎的同學中有![]() 來自七年級,有
來自七年級,有![]() 來自九年級,其他同學均來自八年級.現準備從獲得一等獎的同學中任選2人參加市級鋼筆書法大賽,請通過列表或畫樹狀圖的方法求所選出的2人中既有八年級同學又有九年級同學的概率.
來自九年級,其他同學均來自八年級.現準備從獲得一等獎的同學中任選2人參加市級鋼筆書法大賽,請通過列表或畫樹狀圖的方法求所選出的2人中既有八年級同學又有九年級同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=![]() (x-h)2+k的頂點在x軸上,其對稱軸與直線y=x交于點A(1,1),點P是拋物線上一點,以P為圓心,PA長為半徑畫圓,⊙P交x軸于B、C兩點.
(x-h)2+k的頂點在x軸上,其對稱軸與直線y=x交于點A(1,1),點P是拋物線上一點,以P為圓心,PA長為半徑畫圓,⊙P交x軸于B、C兩點.
⑴h= ,k= ;
⑵①當點P在頂點時,BC= ;
②BC的值是否隨P點橫坐標的變化而變化?如果變化,請說明理由,如果不變化,請求出這個值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,點
中,點![]() 是對角線
是對角線![]() 上一動點,連接
上一動點,連接![]() ,作
,作![]() 分別交
分別交![]() 于點
于點![]() ,
,![]() 于點
于點 ![]() .
.
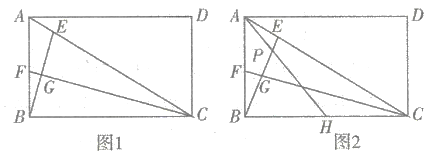
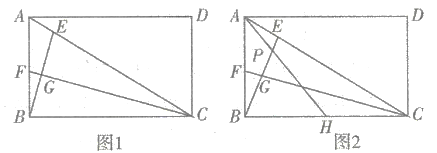
(1)如圖1,若![]() 恰好平分
恰好平分![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() 交
交![]() 于點
于點 ![]() .
.
求證:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,點
中,點![]() 是對角線
是對角線![]() 上一動點,連接
上一動點,連接![]() ,作
,作![]() 分別交
分別交![]() 于點
于點![]() ,
,![]() 于點
于點 ![]() .
.
(1)如圖1,若![]() 恰好平分
恰好平分![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() 交
交![]() 于點
于點 ![]() .
.
求證:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
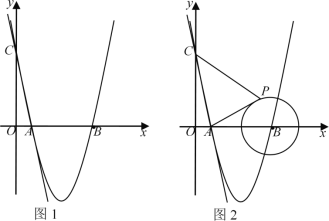
【題目】如圖1,在平面直角坐標系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,拋物線
兩點,拋物線![]() 經過
經過![]() 、
、![]() 兩點,與
兩點,與![]() 軸的另一個交點為
軸的另一個交點為![]() .
.
(1)求拋物線的解析式及![]() 點坐標;
點坐標;
(2)若點M為x軸下方拋物線上一動點,連接MA、MB、BC,當點M運動到某一位置時,四邊形AMBC面積最大,求此時點M的坐標及四邊形AMBC的面積;
(3)如圖2,若![]() 點是半徑為2的⊙
點是半徑為2的⊙![]() 上一動點,連接
上一動點,連接![]() 、
、![]() ,當點
,當點![]() 運動到某一位置時,
運動到某一位置時,![]() 的值最小為_________.(直接寫出結果)
的值最小為_________.(直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
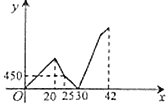
【題目】小杰早上從家勻速步行去學校,走到途中發現英語書忘在家里了,隨即打電話給爸爸,爸爸立即送英語書去,小杰掉頭以原速往回走,幾分鐘后,路過一家文具店,此時還未遇到爸爸,小杰便在文具店購買了幾個筆記本,剛付完款,爸爸剛好趕到,將英語書交給了小杰(途中小杰打電話、小杰的爸爸找英語書的時間忽略不計):然后,爸爸原速返回,同時小杰把速度提高到原來的![]() 前往學校,爸爸到家后,過一會小杰才到達學校.兩人之間的距離
前往學校,爸爸到家后,過一會小杰才到達學校.兩人之間的距離![]() (米)與小杰從家出發的時間
(米)與小杰從家出發的時間![]() (分鐘)的函數關系如圖所示,則家與學校相距______米.
(分鐘)的函數關系如圖所示,則家與學校相距______米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)探究發現:下面是一道例題及解答過程,請補充完整:
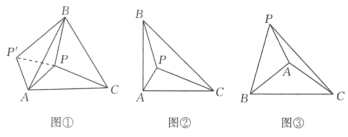
如圖①在等邊△ABC內部,有一點P,若∠APB=150°,求證:AP2+BP2=CP2
證明:將△APC繞A點逆時針旋轉60°,得到△AP’B,連接PP’,則△APP’為等邊三角形
∴∠APP’=60° ,PA=PP’ ,PC=
∵∠APB=150°,∴∠BPP’=90°
∴P’P2+BP2= ,即PA2+PB2=PC2
(2)類比延伸:如圖②在等腰△ABC中,∠BAC=90°,內部有一點P,若∠APB=135°,試判斷線段PA,PB,PC之間的數量關系,并證明.
(3)聯想拓展:如圖③在△ABC中,∠BAC=120°,AB=AC,點P在直線AB上方,且∠APB=60°,滿足(kPA)2+PB2=PC2(其中k>0),請直接寫出k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com