
【題目】反比例函數y= ![]() 與一次函數y=kx﹣k+2在同一直角坐標系中的圖象可能是( )
與一次函數y=kx﹣k+2在同一直角坐標系中的圖象可能是( )
A.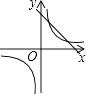
B.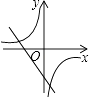
C.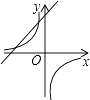
D.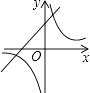
【答案】D
【解析】解:A、如圖所示,反比例函數圖象經過第一、三象限,則k>0,所以一次函數圖象必定經過第一、三象限,與圖示不符,故本選項錯誤; B、如圖所示,反比例函數圖象經過第二、四象限,則k<0.﹣k+2>0,所以一次函數圖象經過第一、二、四象限,與圖示不符,故本選項錯誤;
C、如圖所示,反比例函數圖象經過第二、四象限,則k<0.﹣k+2>0,所以一次函數圖象經過第一、二、四象限,與圖示不符,故本選項錯誤;
D、如圖所示,反比例函數圖象經過第一、三象限,則k>0,所以一次函數圖象必定經過第一、三象限,與圖示一致,故本選項正確;
故選:D.
【考點精析】本題主要考查了一次函數的圖象和性質和反比例函數的圖象的相關知識點,需要掌握一次函數是直線,圖像經過仨象限;正比例函數更簡單,經過原點一直線;兩個系數k與b,作用之大莫小看,k是斜率定夾角,b與Y軸來相見,k為正來右上斜,x增減y增減;k為負來左下展,變化規律正相反;k的絕對值越大,線離橫軸就越遠;反比例函數的圖像屬于雙曲線.反比例函數的圖象既是軸對稱圖形又是中心對稱圖形.有兩條對稱軸:直線y=x和 y=-x.對稱中心是:原點才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】甲、乙二人從同一地點出發,同向而行,甲乘車,乙步行.如果乙先走20 km,那么甲用1 h就能追上乙;如果乙先走1 h,那么甲只用15 min就能追上乙.求甲、乙二人的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
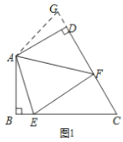
【題目】“半角型”問題探究:如圖1,在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,且∠EAF=60°,探究圖中線段BE,EF,FD之間的數量關系.小明同學的方法是將△ABE繞點A逆時針旋轉120°到△ADG的位置,然后再證明△AFE≌△AFG,從而得出結論:EF=BE+DF
(1)如圖2,在四邊形ABCD中,AB=AD,∠B +∠D=180°,E,F分別是邊BC,CD上的點,且∠EAF=![]() ∠BAD,上述結論是否仍然成立,并說明理由.
∠BAD,上述結論是否仍然成立,并說明理由.
(2)實際應用:
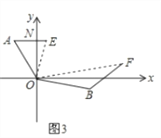
如圖3,在某次軍事演習中,艦艇甲在指揮中心(O處)北偏西30°的A處,艦艇乙在指揮中心南偏東70°的B處,并且兩艦艇到指揮中心的距離相等,接到行動指令后,艦艇甲向正東方向以60海里/小時的速度前進,艦艇乙沿北偏東50°的方向以80海里/小時的速度前進1.5小時后,指揮中心觀測到甲、乙兩艦艇分別到達E,F處,且兩艦艇之間的夾角為70°,試求此時兩艦艇之間的距離?

拓展提高
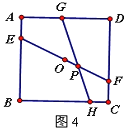
(3)如圖4,邊長為5的正方形ABCD中,點E、F分別在AB、CD上,AE=CF=1,O為EF的中點,動點G、H分別在邊AD、BC上,EF與GH的交點P在O、F之間(與0、F不重合),且∠GPE=45°,設AG=m,求m的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學興趣小組測量校園內旗桿的高度,有以下兩種方案:
方案一:小明在地面上直立一根標桿![]() ,沿著直線
,沿著直線![]() 后退到點
后退到點![]() ,使眼睛
,使眼睛![]() 、標桿的頂點
、標桿的頂點![]() 、旗桿的頂點
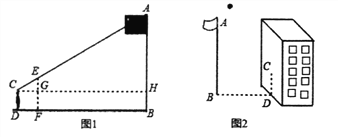
、旗桿的頂點![]() 在同一直線上(如圖1).測量:人與標桿的距離
在同一直線上(如圖1).測量:人與標桿的距離![]() =1 m,人與旗桿的距離
=1 m,人與旗桿的距離![]() =16m,人的目高和標桿的高度差
=16m,人的目高和標桿的高度差![]() =0.9m,人的高度
=0.9m,人的高度![]() =1.6m.
=1.6m.
方案二:小聰在某一時刻測得1米長的竹竿豎直放置時影長1.5米,在同時刻測量旗桿的影長時,因旗桿靠近一樓房,影子不全落在地面上,有一部分落在墻上,他測得落在地面上影長為21米,留在墻上的影高為2米(如圖2).
請你結合上述兩個方案,選擇其中的一個方案求旗桿的高度。我選擇方案 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算題
(1)﹣10﹣(﹣16)+(﹣24);
(2)﹣3.5÷![]() ×(﹣
×(﹣![]() )×|﹣
)×|﹣![]() |
|
(3)(![]() ﹣
﹣![]() +
+![]() )×(﹣36)
)×(﹣36)
(4)(﹣1)3+[42﹣(l﹣32)×2]
查看答案和解析>>
科目:初中數學 來源: 題型:
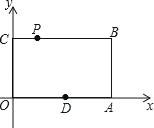
【題目】如圖,在平面直角坐標系中,矩形OABC的頂點A、C的坐標分別為(6,0)、(0,4),點P是線段BC上的動點,當△OPA是等腰三角形時,則P點的坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知 A=2 x2+3xy﹣2x﹣1,B= x2﹣xy﹣1.
(1)化簡:4A﹣(2B+3A),將結果用含有 x、y 的式子表示;
(2)若式子 4A﹣(2B+3A)的值與字母 x 的取值無關,求 y3+![]() A﹣
A﹣ ![]() B 的值.
B 的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一條數軸在原點O和點B處各折一下,得到一條“折線數軸”.圖中點A表示﹣11,點B表示10,點C表示18,我們稱點A和點C在數軸上相距29個長度單位.動點P從點A出發,以2單位/秒的速度沿著“折線數軸”的正方向運動,從點O運動到點B期間速度變為原來的一半,之后立刻恢復原速;同時,動點Q從點C出發,以1單位/秒的速度沿著數軸的負方向運動,從點B運動到點O期間速度變為原來的兩倍,之后也立刻恢復原速.設運動的時間為t秒.

問:(1)動點P從點A運動至C點需要多少時間?
(2)P、Q兩點相遇時,求出相遇點M所對應的數是多少;
(3)求當t為何值時,P、O兩點在數軸上相距的長度與Q、B兩點在數軸上相距的長度相等.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com