
【題目】如圖,數軸的單位長度為1.
![]()
(1)如果點B,D表示的數互為相反數,那么圖中點A、點D表示的數分別是 、 ;
(2)當點B為原點時,在數軸上是否存在點M,使得點M到點A的距離是點M到點D的距離的2倍,若存在,請求出此時點M所表示的數;若不存在,說明理由;
(3) 在(2)的條件下,點A、點C分別以2個單位長度/秒和0.5個單位長度同時向右運動,同時點P從原點出發以3個單位長度/秒的速度向左運動,當點A與點C之間的距離為3個單位長度時,求點P所對應的數是多少?
【答案】(1)﹣4,2 ;(2)2或10 ;(3)﹣18或﹣4.
【解析】
試題(1)由點B,D表示的數互為相反數,所以點B為﹣2,D為2,則點A為﹣4;
(2)存在,分兩種情況討論解答;
(3)設當點A與點C之間的距離為3個單位長度時,運動時間為t,A點運動到:﹣2+2t,C點運動到:3+0.5t,由AC=3,分類討論,即可解答.
試題解析:解:(1)∵點B,D表示的數互為相反數,∴點B為﹣2,D為2,∴點A為﹣4,故答案為:﹣4,2;
(2)存在,如圖:

當點M在A,D之間時,設M表示的數為x,則x﹣(﹣2)=2(4﹣x)
解得:x=2,當點M在A,D右側時,則x﹣(﹣2)=2(x﹣4),解得:x=10,所以點M所表示的數為2或10;
(3)設當點A與點C之間的距離為3個單位長度時,運動時間為t,A點運動到:﹣2+2t,C點運動到:3+0.5t,①﹣2+2t﹣(3+0.5t)=3,解得:t=6,所以P點對應運動的單位長度為:3×6=18,所以點P表示的數為﹣18.
②3+0.5t﹣(﹣2+2t)=3,解得:t=![]() ,所以P點對應運動的單位長度為:3×
,所以P點對應運動的單位長度為:3×![]() =4,所以點P表示的數為﹣4.
=4,所以點P表示的數為﹣4.
答:點P表示的數為﹣18或﹣4.


科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC、BD相交于點O,過點D作對角線BD的垂線交BA的延長線于點E.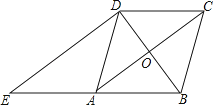
(1)證明:四邊形ACDE是平行四邊形;
(2)若AC=8,BD=6,求△ADE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在桌面上,有6個完全相同的小正方體對成的一個幾何體,如圖所示.

(1)請畫出這個幾何體的三視圖.
(2)若將此幾何A的表面噴上紅漆(放在桌面上的一面不噴),則三個面上是紅色的小正方體有____個.
(3)若另一個幾何體B與幾何體A的主視圖和左視圖相同,而小正方體個數則比幾何體A多1個,則共有______種添法. 請在圖2中畫出幾何體B的俯視圖可能的兩種不同情形.
(4)若現在你的手頭還有一些相同的小正方體可添放在幾何體A上,要保持主視圖和左視圖不變,則最多可以添___________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下圖為人民公園中的荷花池,現要測量此荷花池兩旁A、B兩棵樹間的距離(我們不能直接量得).請你根據所學知識,以卷尺和測角儀為測量工具設計一種測量方案.
要求:(1)畫出你設計的測量平面圖;
(2)簡述測量方法,并寫出測量的數據(長度用![]() …表示;角度用
…表示;角度用![]() …表示);
…表示);
(3)根據你測量的數據,計算A、B兩棵樹間的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分線BE交AC的延長線于點E.
(1)求∠CBE的度數;
(2)過點D作DF∥BE,交AC的延長線于點F,求∠F的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
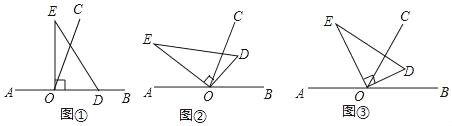
【題目】如圖,以直線AB上一點O為端點作射線OC,使∠BOC=70°,將一個直角三角形的直角頂點放在點O處.(注:∠DOE=90°)
(1)如圖①,若直角三角板DOE的一邊OD放在射線OB上,則∠COE= °;
(2)如圖②,將直角三角板DOE繞點O逆時針方向轉動到某個位置,若OC恰好平分∠BOE,求∠COD的度數;
(3)如圖③,將直角三角板DOE繞點O轉動,如果OD始終在∠BOC的內部,試猜想∠BOD和∠COE有怎樣的數量關系?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題。
(1)計算:﹣22+| ![]() ﹣4|+(
﹣4|+( ![]() )﹣1+2tan60°.
)﹣1+2tan60°.
(2)先化簡,再求值:( ![]() ﹣
﹣ ![]() )÷
)÷ ![]() ,其中x是不等式3x+7>1的負整數解.
,其中x是不等式3x+7>1的負整數解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC繞點A按順時針方向旋轉得到的,連接BE、CF相交于點D. 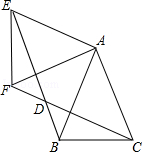
(1)求證:BE=CF;
(2)當四邊形ACDE為菱形時,求BD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com