【題目】如圖正方形ABCD的邊長為4，E、F分別為DC、BC中點．
（1）求證：△ADE≌△ABF． （2）求△AEF的面積．
【答案】(1)、證明過程見解析；(2)、6.
【解析】
試題分析：(1)、根據正方形的性質以及中點得出DE=DF，結合正方形的性質得出△ADE和△ABF全等；(2)、利用正方形的面積減去三個直角三角形的面積得出△AEF的面積.
試題解析：(1)、∵四邊形ABCD為正方形， ∴AB=AD，∠=90°，DC=CB， ∵E、F為DC、BC中點，
∴DE=
DC，BF=BC， ∴DE=BF， ∵在△ADE和△ABF中，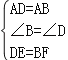
， ∴△ADE≌△ABF（SAS）；
(2)、由題知△ABF、△ADE、△CEF均為直角三角形， 且AB=AD=4，DE=BF=×4=2，CE=CF=×4=2，
∴S△AEF=S正方形ABCD﹣S△ADE﹣S△ABF﹣S△CEF=4×4﹣×4×2﹣
×4×2﹣×2×2=6．
文敬圖書課時先鋒系列答案科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=5，AD=4，BD=DC=3，且DE⊥AB于E，DF⊥AC于點F．
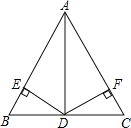
（1）請寫出與A點有關的三個正確結論；
（2）DE與DF在數量上有何關系？并給出證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AB=BC，BE⊥AC于點E，AD⊥BC于點D，∠BAD=45°，AD與BE交于點F，連接CF．
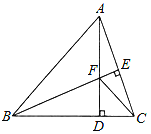
（1）求證：BF=2AE；
（2）若CD=
，求AD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商店出售三種品牌的面粉，袋上分別標有質量為（25±0.1）kg、（25±0.2）kg、（25±0.3）kg的字樣，任意取出兩袋，它們的質量最多相差（ ）
A. 0.4kg B. 0.5kg C. 0.6kg D. 0.8kg
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】標有﹣3，﹣2，4的三張不透明的卡片，除正面寫有不同的數字外，其余的值都相同，將這三張卡片背面朝上洗勻后，第一次從中隨機抽取一張，并把這張卡片標有的數字記為二次函數解析式y=a（x﹣k）2+b的k值，第二次從余下的兩張卡片中再抽取一張，上面標有的數字記為二次函數解析式的b值．
（1）寫出k為負數的概率；
（2）求二次函數y=a（x﹣k）2+b的圖象上頂點在雙曲線y=﹣
上的概率．（用樹狀圖或列舉法求解）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一元二次方程x2﹣6x﹣5=0配方組可變形為（ ）
A．（x﹣3）2=14 B．（x﹣3）2=4 C．（x+3）2=14 D．（x+3）2=4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com