Question

【題目】如圖，“中國海監50”正在南海海域A處巡邏，島礁B上的中國海軍發現點A在點B的正西方向上，島礁C上的中國海軍發現點A在點C的南偏東30°方向上，已知點C在點B的北偏西60°方向上，且B、C兩地相距120海里．

（1）求出此時點A到島礁C的距離；
（2）若“中海監50”從A處沿AC方向向島礁C駛去，當到達點A′時，測得點B在A′的南偏東75°的方向上，求此時“中國海監50”的航行距離．（注：結果保留根號）

Answer 1

【答案】
（1）

解：如圖所示：

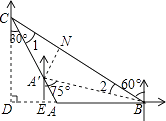
延長BA，過點C作CD⊥BA延長線與點D，

由題意可得：∠CBD=30°，BC=120海里，

則DC=60海里，

故cos30°= = = ，

解得：AC=40 ，

答：點A到島礁C的距離為40 海里

（2）

解：如圖所示：

過點A′作A′N⊥BC于點N，

可得∠1=30°，∠BA′A=45°，A′N=A′E，

則∠2=15°，即A′B平分∠CBA，

設AA′=x，則A′E= x，

故CA′=2A′N=2× x= x，

∵ x+x=40 ，

∴解得：x=60﹣20 ，

答：此時“中國海監50”的航行距離為（60﹣20 ）海里．

【解析】（1）根據題意得出：∠CBD=30°，BC=120海里，再利用cos30°= ，進而求出答案；（2）根據題意結合已知得出當點B在A′的南偏東75°的方向上，則A′B平分∠CBA，進而得出等式求出答案．