
【題目】“水是生命之源”,某城市自來水公司為了鼓勵居民節約用水,規定按以下標準收取水費:
用水量/月 | 單價(元/m3) |
不超過20m3 | 2.8 |
超過20m3的部分 | 3.8 |
另:每立方米用水加收0.2元的城市污水處理費
(1)如果1月份某用戶用水量為19m3 , 那么該用戶1月份應該繳納水費元.
(2)某用戶2月份共繳納水費80元,那么該用戶2月份用水多少m3?
(3)若該用戶水表3月份出了故障,只有70%的用水量記入水表中,這樣該用戶在3月份只繳納了58.8元水費,問該用戶3月份實際應該繳納水費多少元?
【答案】
(1)57
(2)解:設該用戶2月份用水xm3 , 由題意,得20×3+4×(x﹣20)=80,
解得:x=25.
答:該用戶2月份用水25m3
(3)解:設該用戶3月份實際用水am3
因為58.8<20×3,所以該用戶上交水費的單價為3元/m3 .
由題意,得70%a×3=58.8.
解得:a=28.
因為28>20,
所以該用戶3月份實際應該繳納水費為:20×3+4×(28﹣20)=92元.
答:該用戶3月份實際應該繳納水費92元
【解析】解:(1)根據表格數據可知:
該用戶1月份應該繳納水費19×3=57元;
(1)19<20,因此水費單價為為3元/m3 . 根據用水量![]() 水費單價,計算即可得出答案。
水費單價,計算即可得出答案。
(2)由于20![]() 3<80,因此2月份用水量超過20m3,等量關系是:20m3水的費用+4×超過20m3部分的水量=80,設未知數,建立方程求解即可。
3<80,因此2月份用水量超過20m3,等量關系是:20m3水的費用+4×超過20m3部分的水量=80,設未知數,建立方程求解即可。
(3)由于58.8<20×3,所以該用戶上交水費的單價為3元/m3 . 設未知數建立方程,求解得出該用戶3月份實際用水量,再算出該用戶3月份實際應該繳納的水費。


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】下列說法正確的有( )
①對角線互相平分且垂直的四邊形是菱形;
②一組對邊平行,一組對邊相等的四邊形是平行四邊形;
③有一個角是直角的四邊形是矩形;
④對角線相等且垂直的四邊形是正方形
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P是Rt△ABC斜邊AB上一動點(不與A,B重合),分別過A,B向直線CP作垂線,垂足分別為E,F.
(1)如圖1,當點P為AB的中點時,連接AF,BE.求證:四邊形AEBF是平行四邊形; 
(2)如圖2,當點P不是AB的中點,取AB的中點Q,連接EQ,FQ.試判斷△QEF的形狀,并加以證明. 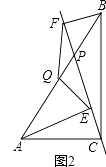
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解外來務工子女就學情況,某校對七年級各班級外來務工子女的人數情況進行了統計,發現各班級中外來務工子女的人數有1名、2名、3名、4名、5名、6名共六種情況,并制成如下兩幅統計圖:
(1)求該校七年級平均每個班級有多少名外來務工子女?并將該條形統計圖補充完整;
(2)學校決定從只有2名外來務工子女的這些班級中,任選兩名進行生活資助,請用列表法或畫樹狀圖的方法,求出所選兩名外來務工子女來自同一個班級的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
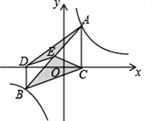
【題目】如圖,點A,B在反比例函數![]() (k>0)的圖象上,AC⊥x軸,BD⊥x軸,垂足C,D分別在x軸的正、負半軸上,CD=k,已知AB=2AC,E是AB的中點,且△BCE的面積是△ADE的面積的2倍,則k的值是______.
(k>0)的圖象上,AC⊥x軸,BD⊥x軸,垂足C,D分別在x軸的正、負半軸上,CD=k,已知AB=2AC,E是AB的中點,且△BCE的面積是△ADE的面積的2倍,則k的值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以下四種沿AB折疊的方法中,不一定能判定紙帶兩條邊線a,b互相平行的是( )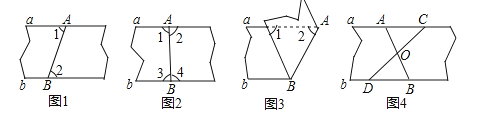
A.如圖1,展開后測得∠1=∠2
B.如圖2,展開后測得∠1=∠2且∠3=∠4
C.如圖3,測得∠1=∠2
D.如圖4,展開后再沿CD折疊,兩條折痕的交點為O,測得OA=OB,OC=OD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com